BTree、B+Tree和LSM-Tree等数据结构是数据库存储引擎中及其常用的数据结构,本文讲解了这些数据结构的特点和异同;
视频地址:
BTree、B+Tree和LSM-Tree常用存储引擎数据结构总结
引言
我们知道,数据有三大模块:
- 存储;
- 事物;
- SQL解析、优化;
其中,存储模块负责数据在磁盘、内存上的存储、检索和管理,并向上层提供细粒度的数据操作接口;
同时,由于存储模块和其他模块耦合较少,因此可以将其抽象为一个专用的数据库组件,即:存储引擎;
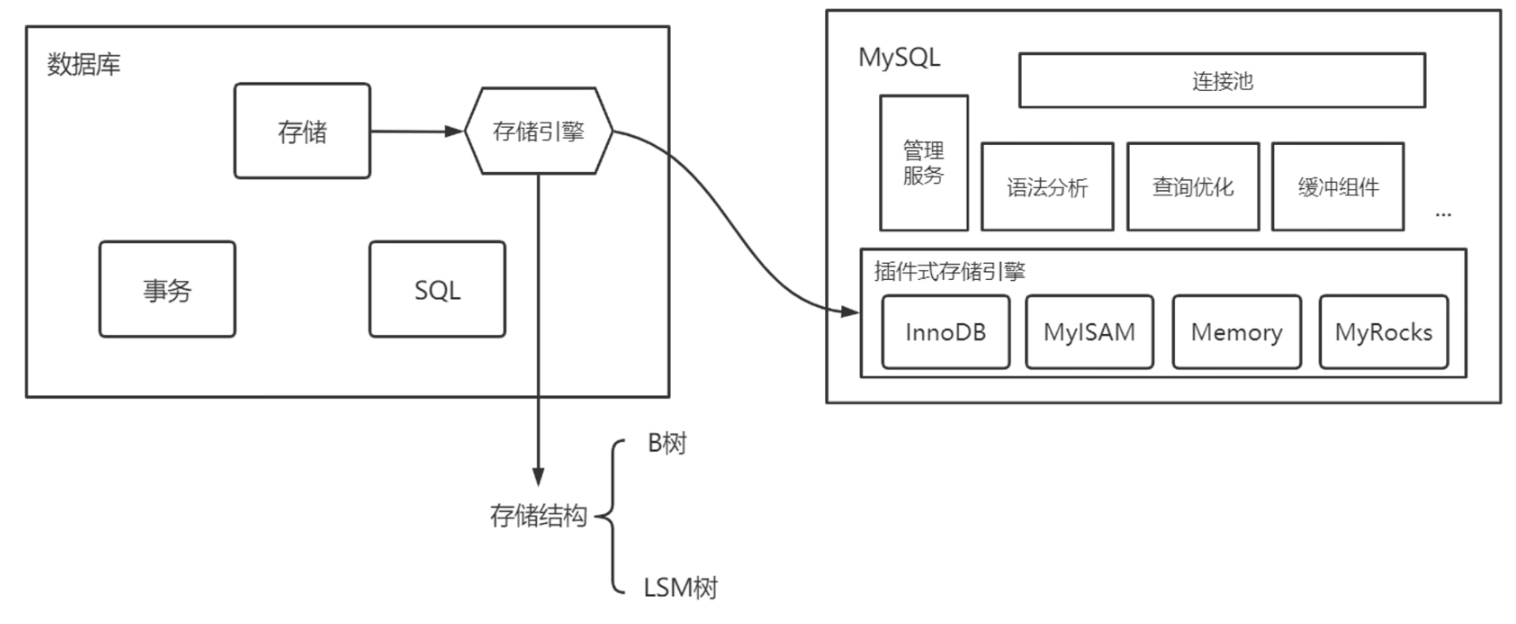
目前,很多数据库都支持可插拔的存储引擎,例如:MySQL支持:InnoDB、MyISAM、Memory、基于RocksDB的MyRocks等;
对于存储而言,最重要的就是数据存储的结构(也即,数据结构!);
内存、缓存、读写流程的任何设计都是建立在存储结构的基础之上的!因此,存储结构和存储引擎的特性和性能关系非常密切!
相比于存储引擎而言,目前的存储结构并不是很多:
BTree 作为一个非常适合磁盘的存储结构,自关系型数据库诞生以来,一直占据主流;
而近些年来随着分布式技术的发展以及固态硬盘的发展(随机读写性能的急剧提升),LSM-Tree 越来越火热;
存储引擎与存储结构
存储引擎要存储什么?
首先要明确,存储引擎要存储什么?
由于存储引擎是基于文件系统的,因此存储引擎是将一条条数据转换为具体的文件进行存储;
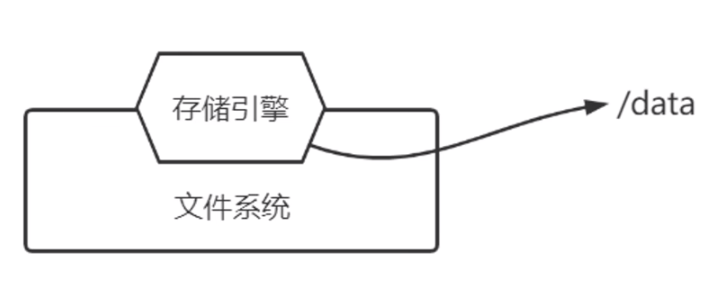
很多数据库的 /data 目录下就存储有数据文件;
除了存储原始数据外,我们也需要将数据库中的索引组织为文件来存储;
因此,存储引擎要存储:
- 数据文件;
- 索引文件;
存储引擎数据文件的组织形式
目前主流的数据文件组织形式有三种:
- 索引组织表;
- 堆组织表;
- 哈希组织表;
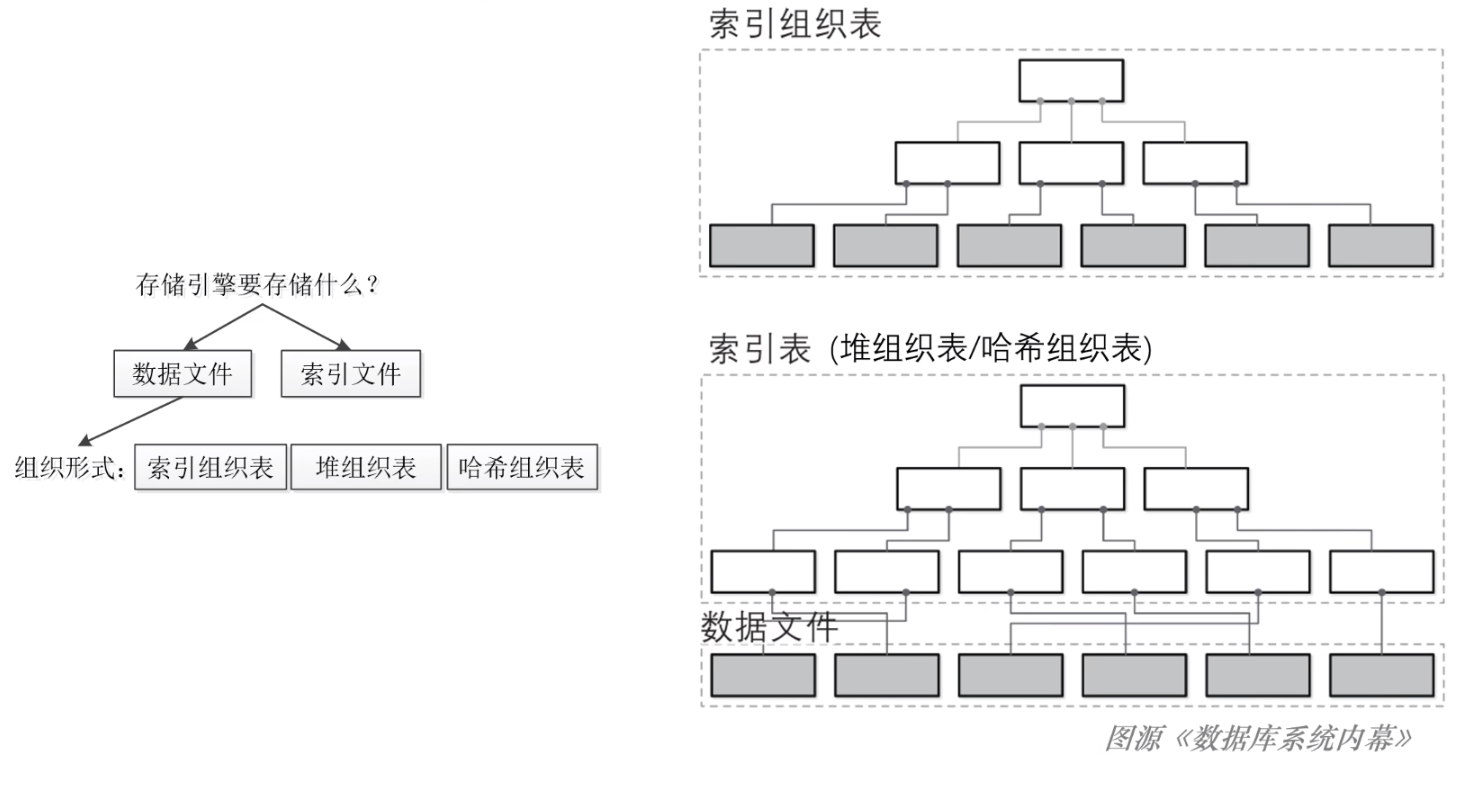
索引组织表:
- 索引组织表将数据文件和索引文件合并在一起,如上图右上部分:
- 索引组织表直接将数据记录存储在索引文件内部;
- 如:InnoDB存储引擎;
堆组织表:
- 堆组织表的数据文件是一个“无序堆”(一堆数据)的数据结构,其中的数据记录一般不需要有特定顺序;
- 虽然堆组织表中的数据文件是无序的,但是我们可以通过索引文件中的索引结构来快速定位数据在堆中的位置;
- 如:Oracle、PostgreSQL;
哈希组织表:
- 将记录分散存储在一个个桶中,每条记录主键的 Hash 值来确定记录属于哪个桶;
- 记录 Hash 值的部分就是索引文件,记录 Hash 结果的部分是数据文件;
目前主流的存储引擎基本都没有使用哈希组织表;
堆组织表因为数据的插入是无序的,而索引组织表需要根据索引的顺序插入数据,因此通常情况下:
堆组织表的写入性能强于索引组织表,读取性能弱于索引组织表;
但是,数据文件的组织形式对于性能的影响还是比较小的,因为大多数都使用的是B树索引;
而索引作为读写数据的主要入口,索引文件的组织形式对于存储引擎的性能关系更加密切!
例如:
将索引文件的组织形式从 BTree 换为 LSM-Tree,则性能差异会非常大!
因此,通常情况下要重点关注的其实是:索引文件的组织形式!
存储结构分类和发展历程
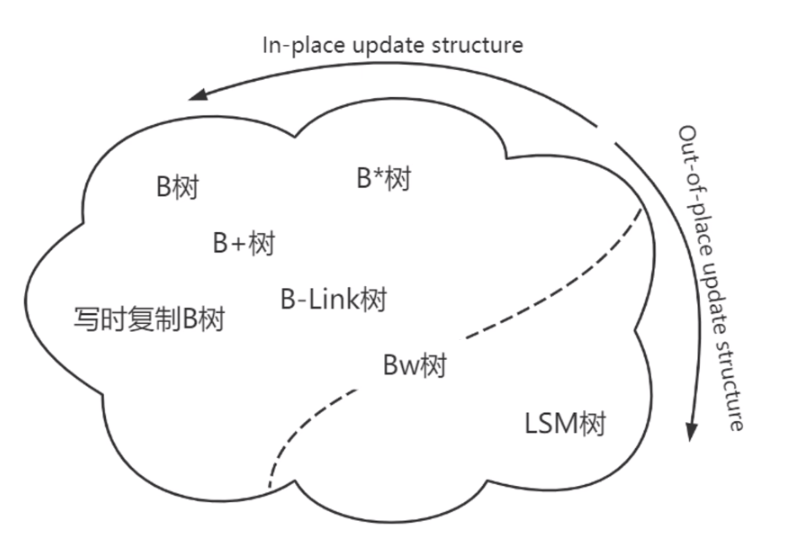
目前,BTree和LSM-Tree 这两类存储结构在存储引擎中被使用的最为广泛,他们也分别对应了:
- In-place update(BTree、B+Tree):就地更新结构,直接覆盖旧记录来存储更新内容;
- Out-of-place update(LSM-Tree):异位更新结构,会将更新的内容存储到新的位置,而不是直接覆盖旧的条目;
如下图所示;
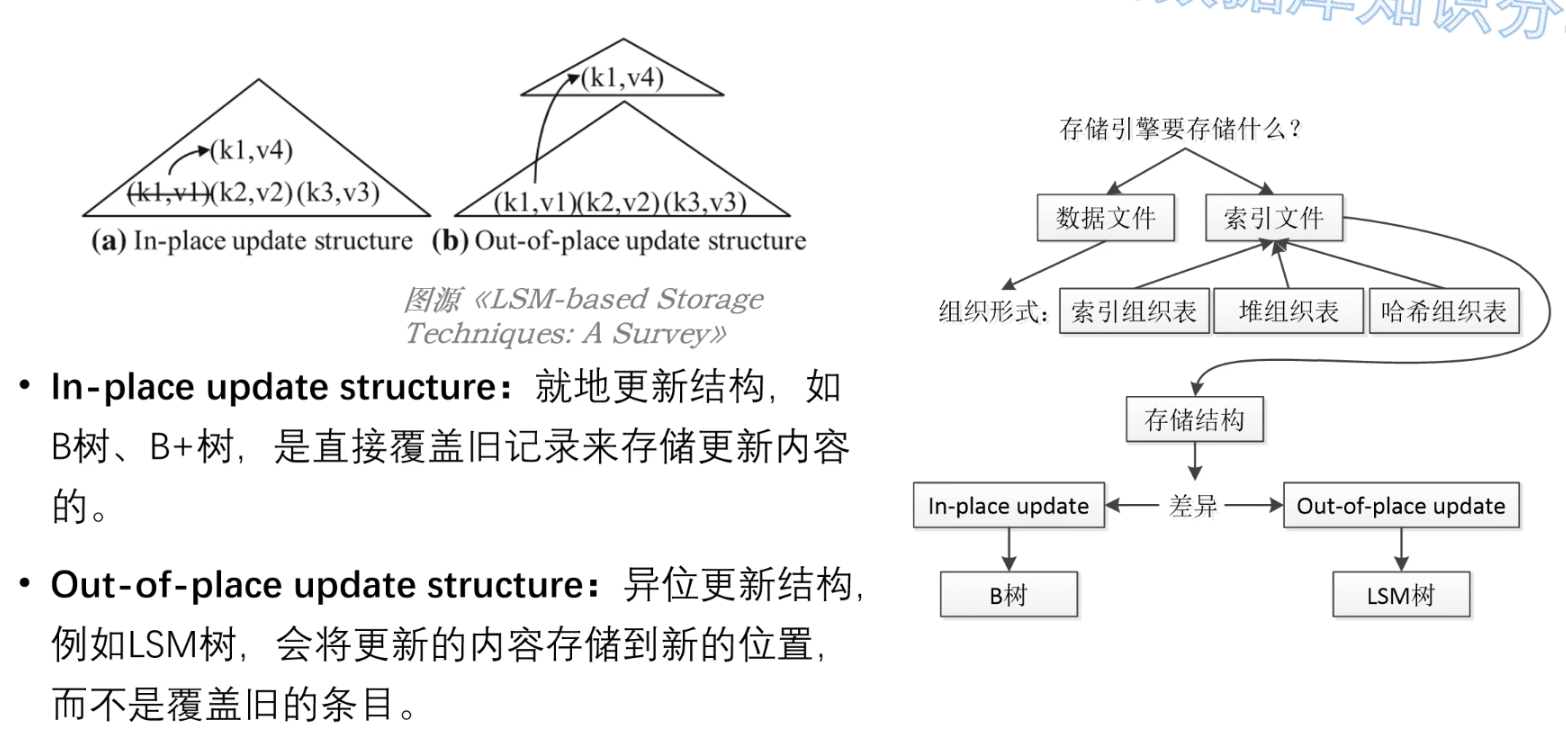
In-place update
In-place update 对应于图(a)部分;
为了更新 key 为 k1 的 value,In-place 操作会直接涂改掉 k1,并且直接在原位置写入 (k1, v4);
这种就地更新的结构,由于只会存储每个记录最新的版本,因此往往读性能更优,但是写入的代价会变大,因为更新会导致随机 IO;
Out-of-place update
Out-of-place update 对应于图(b)部分,在更新时,会将更新的内容存储到新的位置,而非覆盖旧的条目;
在更新 k1 的 value 并不会修改掉原(k1, v1)键值对,而是在一个新的位置写入一条新的纪录(k1, v4);
由于这种设计通常是顺序写入,因此写入性能会更高,但是读性能会被牺牲掉:因为可能要扫描多个位置,才能读到想要的结果;
例如:level-db 在读取时,会自上而下一层一层的读取直到找到首个匹配的记录;
此外,这种数据结构还需要一个数据整合过程,来防止数据的无限膨胀,即:Compaction 过程;
存储结构发展历程
1970年,Rudolf Bayer 教授在《Organization and Maintenance of Large Ordered Indices》一文中提出了BTree,从他的基础上诞生了 B+Tree 等许多变种;
1996年,《The Log-Structured Merge-Tree(LSM-Tree)》论文发表,LSM-Tree 概念正式诞生;
2003年,《The Google File System(GFS)》发表,对追加的一致性保证强于改写,此后的分布式文件系统基本都更推荐使用追加写文件;
2006年,《Bigtable:A distributed strorage system for structured data》发表,相当于一个在 GFS 基础上搭建的不支持事务的分布式存储引擎,而其中的存储引擎采用的就是类似 LSM-Tree 的结构;
2014年左右,SSD 开始进入大规模商用,LSM-Tree 在SSD 上读性能得到很大提升(随机读减少了普通硬盘的寻道时间),同时LSM-Tree对SSD上的写更加友好(追加写提高了SSD的使用寿命),因此 LSM-Tree 进一步得到发展;
SSD 是基于闪存进行存储的,由于闪存不能直接进行覆盖写,而必须首先擦除闪存块之后才能写入;
因此 LSM-Tree 追加写的特性可以完美契合其特性;
总结一下:
BTree 作为 In-place update 模式的存储结构,在早期机械硬盘结构上表现的最好,因此占据了主流;
而随着分布式(大数据)和 SSD 技术的发展,Out-of-place update 模式的优势逐渐凸显,因此 LSM Tree 应用的越来越广泛;
存储结构的共性特点
存储结构需要的特性
我们有那么多的数据结构,例如:数组、链表、Hash表等,为什么 BTree 或 LSM-Tree 能够作为存储结构呢?
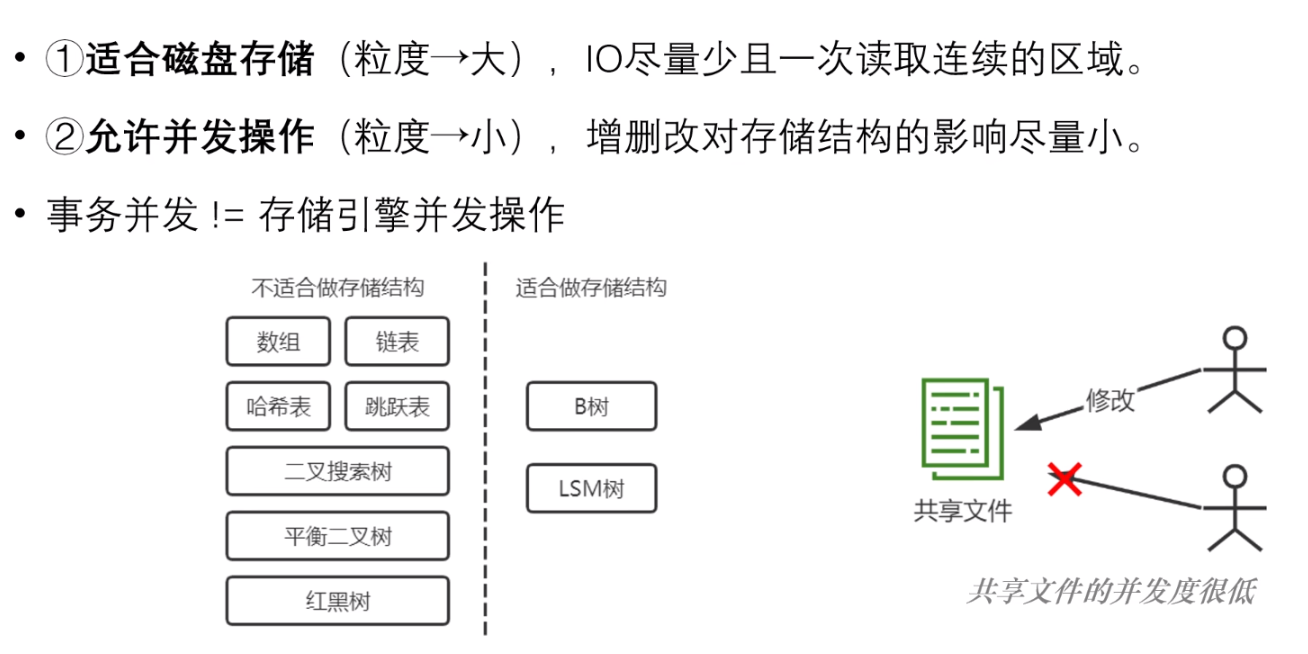
但是大部分都不适合作为磁盘上的存储结构,这需要考虑一下存储结构需要具有的特性:
- 1、适合磁盘存储;
- 2、允许并发操作;
首先,对于磁盘结构,顺序 IO 的性能是远远优于随机 IO 的,因此存储结构涉及到的 IO 次数越少越好,并且尽量一次读取一块连续的区域,因此从这个角度来看,存储结构的一个单元应当越大越好;
同时,存储结构应当允许并发操作,从写入并发避免数据竞争的角度来看,存储结构的单元应当越小越好;
这里所说的并发操作并非数据库事务并发操作,而是内存中的数据结构;
根据上面两个特性再审视一下之前上面列出的内存数据结构不难发现:
- 有1没2,即:只适合磁盘存储的,而不适合并发操作的:大文件、数组,他们都是一大段连续的存储区域,如果要修改,影响面很大,基本上要锁住整个数据结构!
- 有2没1,即:高并发但是不适合磁盘存储的:链表、哈希表、二叉树、红黑树等,他们的修改、写入影响小,但数据结构的粒度也非常小,一般一次只操作几个字节,不适合磁盘 IO;
那么是否存在数据结构同时满足上面两个特性呢?
当然,BTree 就是这么个数据结构;
以BTree为例的In-place存储结构
如下图所示:
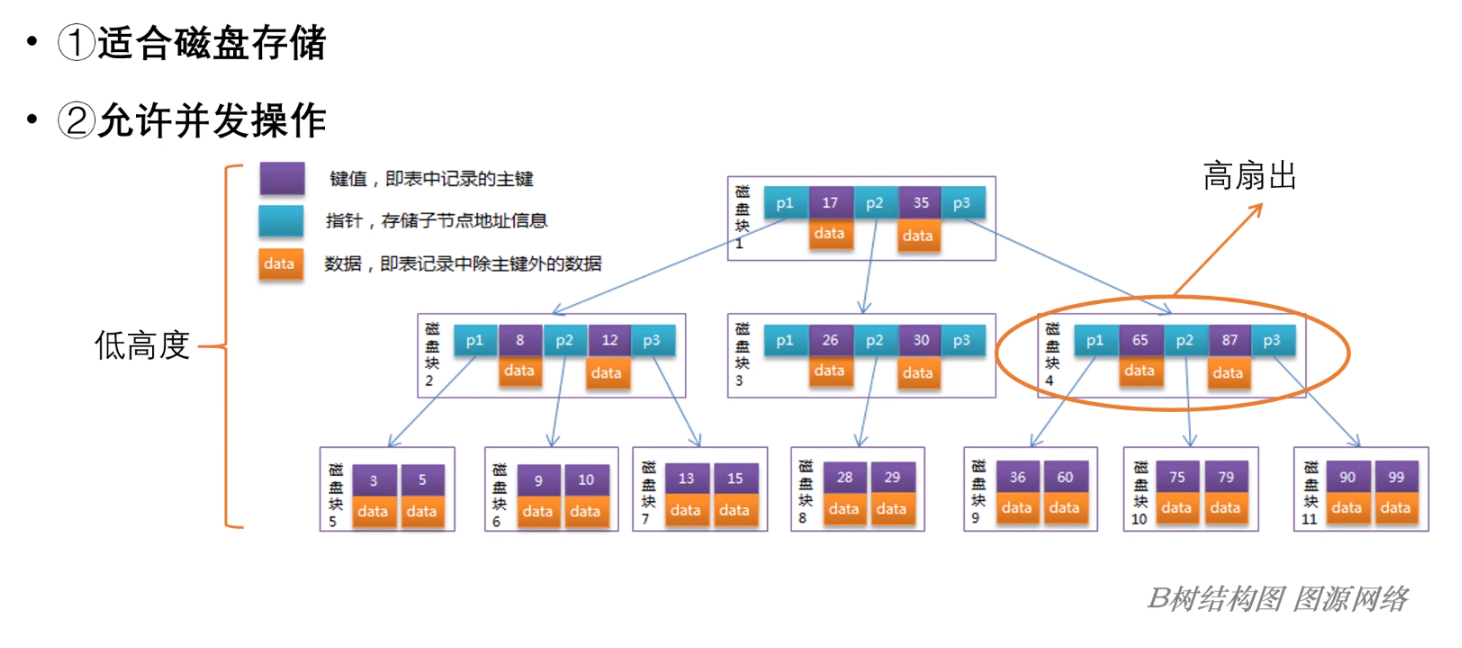
BTree 是一个以页为单位组织的;
首先,InnoDB 存储引擎中页的大小为 16k,一般可以指出几百上千个指针,因而具有高扇出、低高度的特点,从而保证了 BTree 是连续 IO、并且 IO 次数极少,因此适合磁盘存储;
其次,BTree 要修改的单位也是页,因此并发控制的锁在页上,BTree 并发的程度也很高;
但是并非这么简单,虽然 BTree 要修改的单位是页,但是 BTree 存在 SMO(Structure Modification Operation) 操作,即:在增删改操作可能会造成节点的分裂或者合并,此时需要操作多个磁盘块!
当我们向一个页中增加数据超过其大小、或者删除数据使其空间少于二分之一时,就会造成页的分裂或者合并,影响关联节点或者父节点;
同时,上述影响可能还会向上传递,甚至影响到根节点!
SMO 会导致 BTree 的并发能力并不理想;
所以,如果我们想要保证出现 SMO 操作时读写安全的话,就需要对有可能受到 SMO 操作影响的一整条链上所有节点加锁,如下图所示;
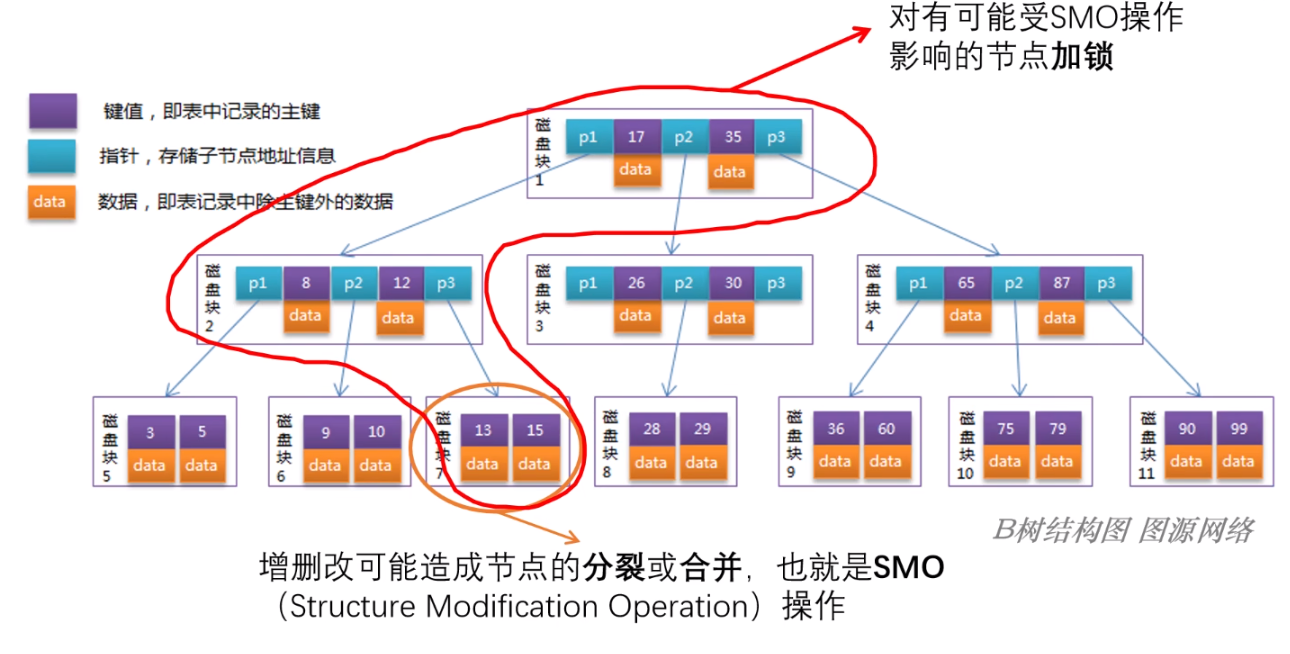
总之,虽然 BTree 有一定的并发能力,但是由于 SMO 的存在使得 BTree 的性能并不高,勉强满足并发要求,但是有很大的优化空间;
Lock和Latch的区别(存储引擎并发操作和事务并发操作的不同)
这里补充一下存储引擎的并发操作和事务并发操作的不同;
假设都以锁机制来控制并发,上面两种机制对应的锁分别称为:Lock 和 Latch;
其中:
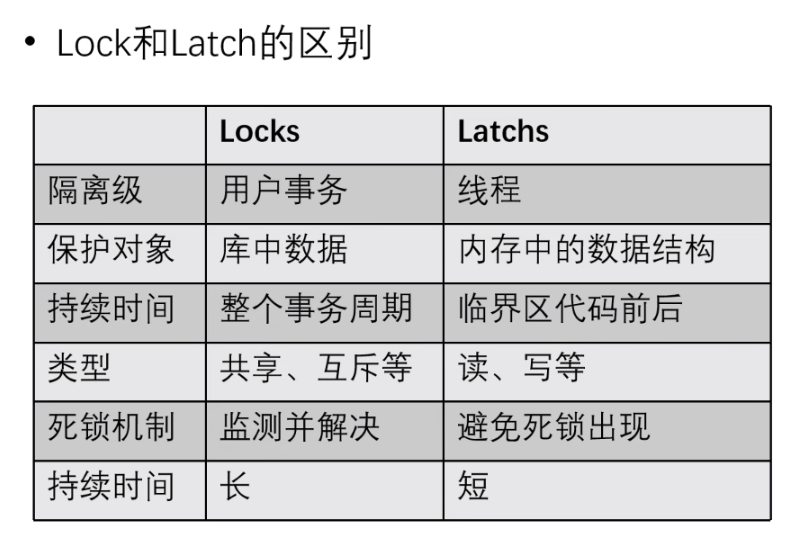
- Lock:用来维持数据库事务的 ACID 特性,事务级隔离,锁住的对象为用户的数据,是一个逻辑概念,例如:共享锁、互斥锁(S、X锁)等;
- Latch:保护数据读取过程中,加载到内存中数据结构的锁,是线程级隔离的锁;主要是防止多个线程并发去修改内存中的共享数据;
例如:
假设修改一行数据,那么首先需要将这行数据所在的页加载至内存中,随后进行修改;
而在修改前,为了防止其他线程也要来修改这页数据,需要使用 Latch 对内存数据进行上锁;加好 Latch 后,可以对数据进行修改;
此时,为了防止在事务进行提交之前,存在其他别的事务读到这行修改后未提交的数据,此时需要对数据增加 Lock;
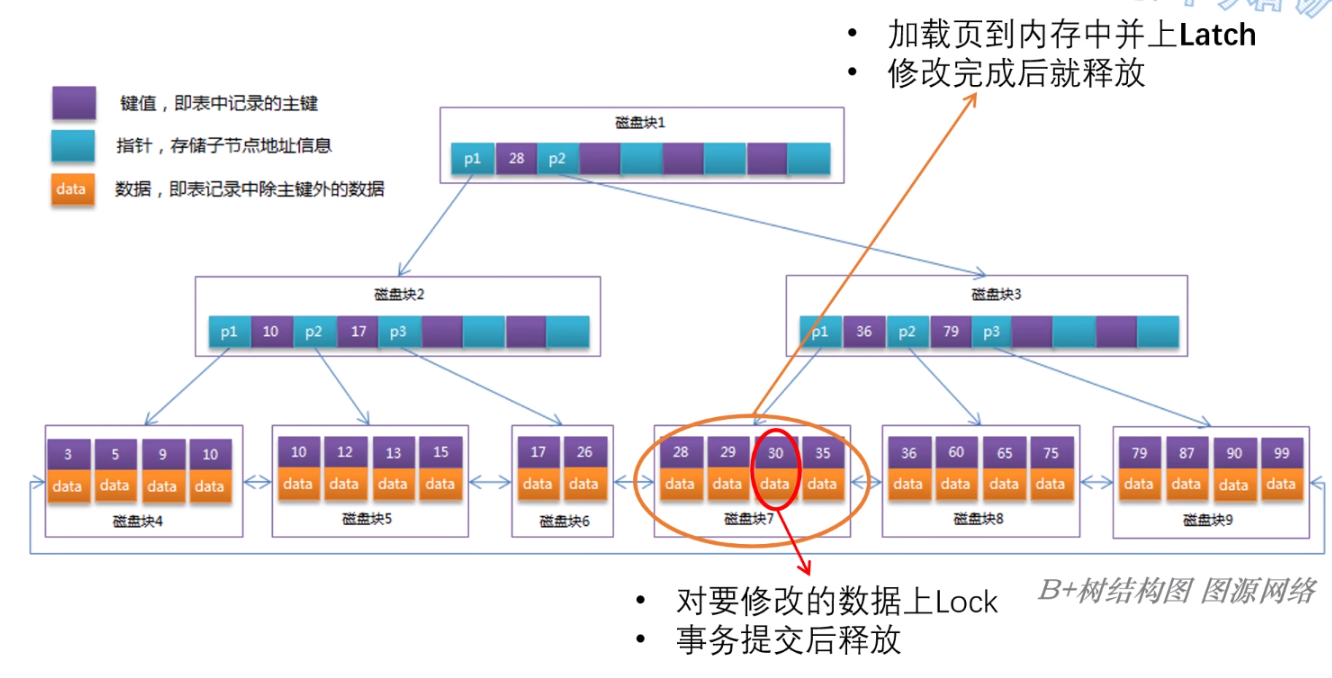
虽然 Latch 锁掉整个页数据,而 Lock 仅仅锁掉单行数据;
但是一旦完成了对这行数据的修改,那么 Latch 锁就可以释放,而 Lock 锁需要等到整个事务提交之后才能够释放!
在数据修改完成到事务提交的这段时间,Lock 就可以发挥作用了!
因此,在对数据库进行操作时,实际上是存在 Latch 和 Lock 两种锁共同生效的!但是对于用户而言,只能感觉到 Lock 锁(即,事务锁);
Latch导致的性能损失
虽然 Latch 的持续时间很短,但是他也会严重影响数据库性能!
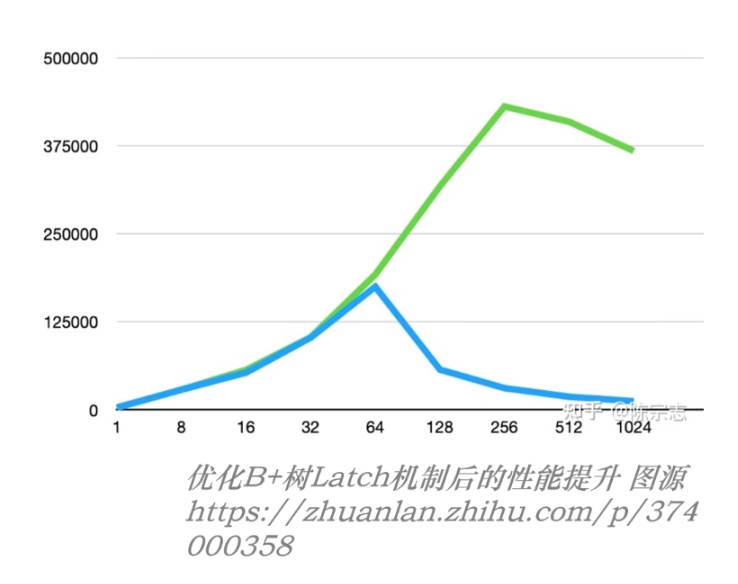
如上图所示为 PolarDB 在优化 InnoDB B+Tree 的 Latch 结构前后的性能对比:蓝色为原 InnoDB、绿色为优化后;
可以看到,在高并发场景下,性能提升接近三倍(即:在优化前执行 INSERT 操作可能只能达到 5w QPS,而优化后可以达到 15w QPS!);
关于这里性能损失的原因,后文会说到!
BTree的各种变种
刚讲了上面的内容,那么 BTree 的各种变种的优化方向大致也就是通过优化下面两个方向来设计的:
- 1、适合磁盘存储(提高粒度),IO 尽量少且一次读取连续的区域;
- 2、允许并发操作(减小粒度),增删改对存储结构的影响尽量小;
| 类型 | 加强方向 |
|---|---|
| B+Tree | 加强1 |
| B-Link Tree | 加强2 |
| Bw Tree | 加强2 |
例如,最出名的 B+Tree 在非叶子节点中仅保留指针(在 BTree 中非叶子结点也存储了行数据),所有的数据都存放在叶子节点,间接减少了树的高度;
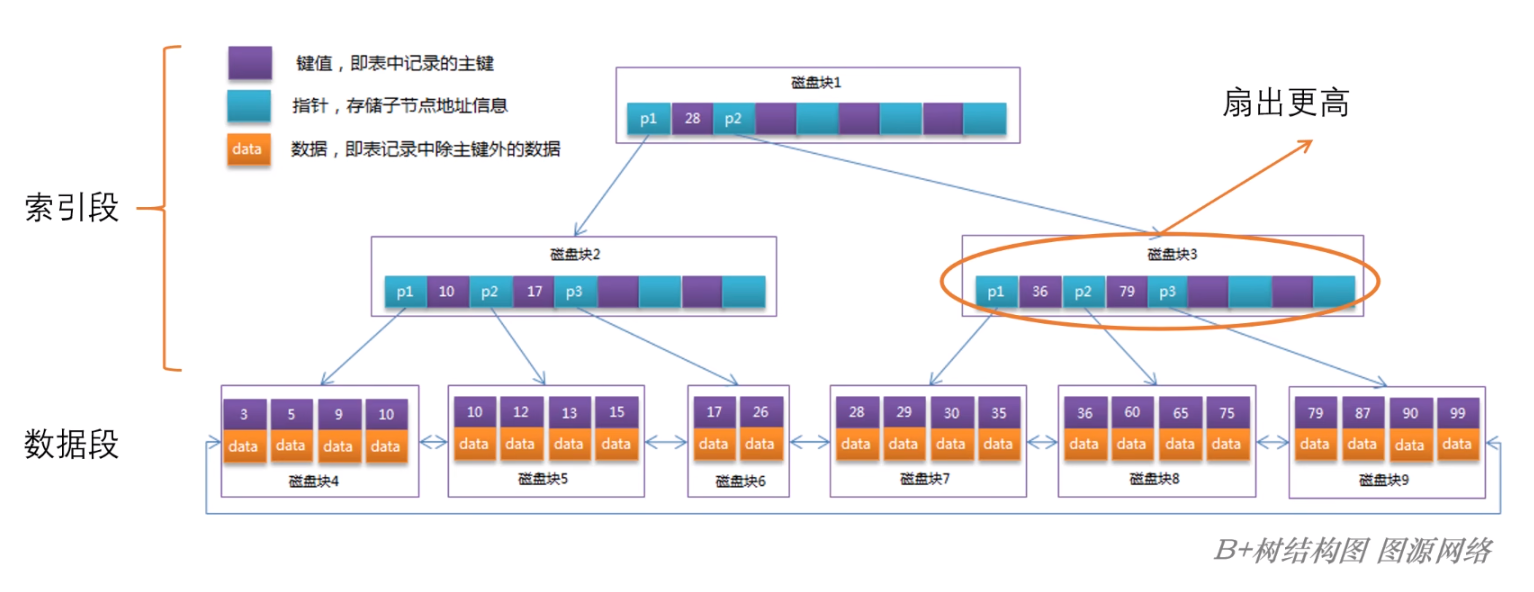
并且这样还可以区分开索引段和数据段,有助于全表扫描时的顺序IO;
总之,提升了 BTree 的特性1;
而 B-Link Tree 对 BTree 的并发控制机制做了很大的改进,提升了特性2;
对于近些年才提出的 Bw-Tree 而言,其采用了类似于 LSM-Tree 的 out-of-place update 方法,追加的写入完全无 Latch 操作(避免多线程并发写),从根本的角度上提升了特性2;
以LSM-Tree为例的Out-of-place存储结构
LSM-Tree基本概念
下面来讲解一下 LSM-Tree 在上面两个特性上的表现;
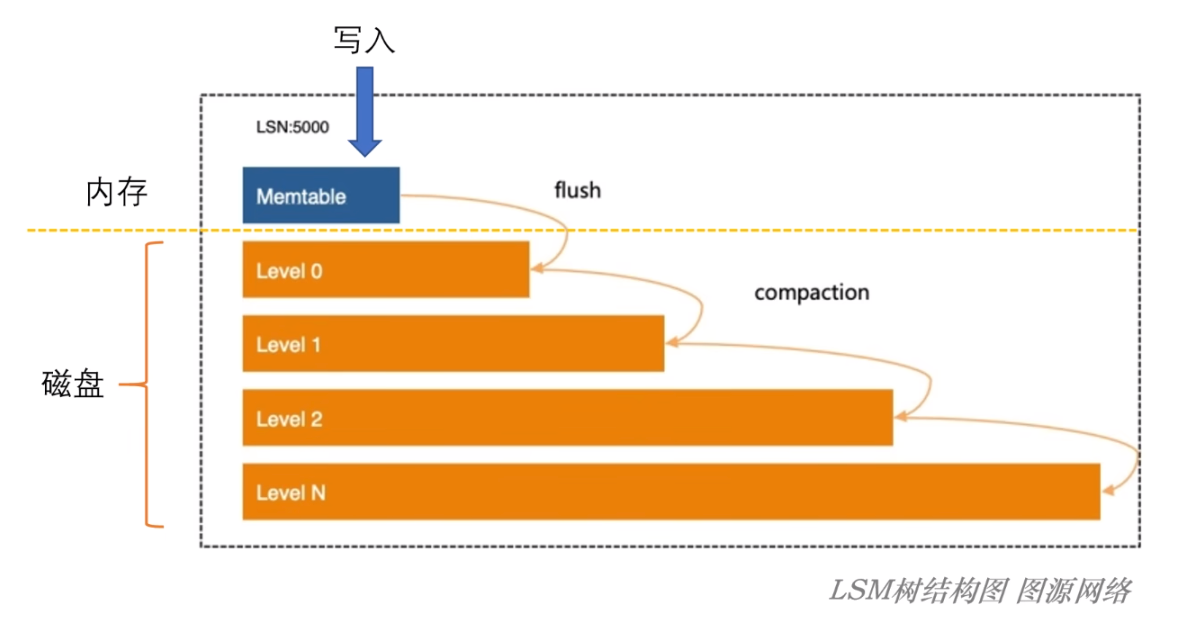
对于 LSM-Tree 的结构而言:
整体是一个分为多层、并且越向下层数据越多的层次树形结构;
对于写操作:
- 所有的写入操作都会首先直接写入内存(write);
- 如果内存写满了,就会直接将内存中刚刚写入的这块数据刷入磁盘中(flush);
- 当向磁盘刷入一定数量的数据之后,将本层数据和下一层数据进行合并、排序、去重;整理后的数据就放在下一层,因此就去除了数据的冗余(compaction);
- Compaction 过程可能会持续多层,并且越下层的数据就越多,最终就形成了 LST-Tree 的整体结构;
下面来看读取操作:
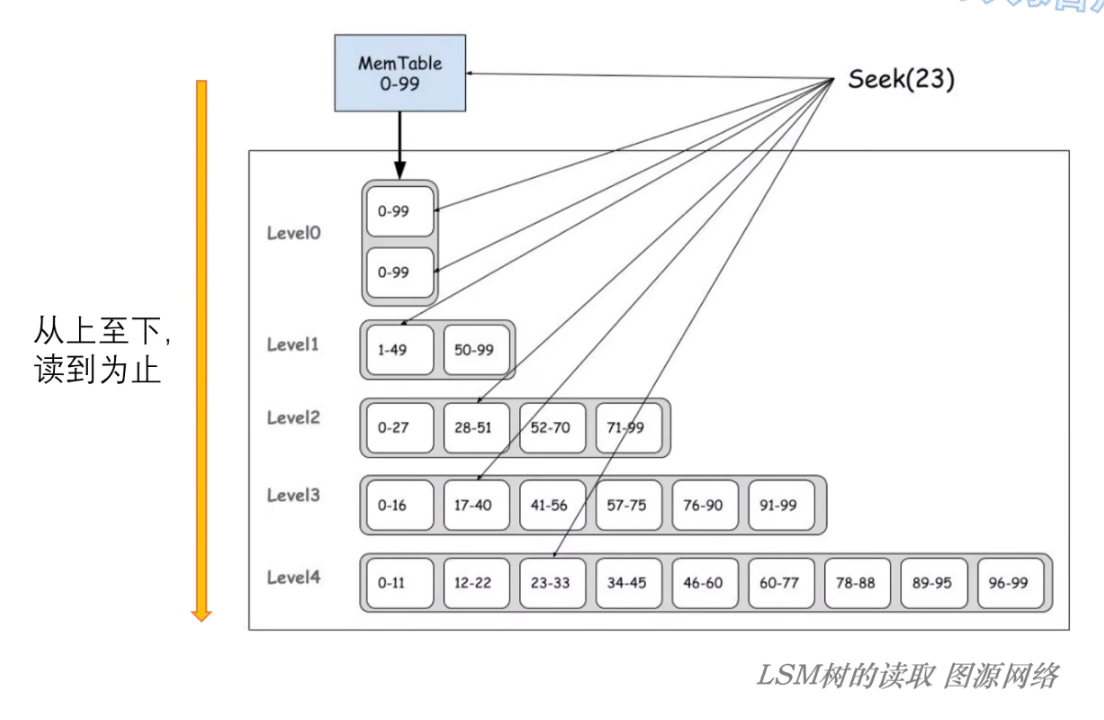
读取的时候需要注意:
由于一个 key 对应的 value 可能会存在于多个层次上,此时需要以最新(更上层的)数据为准;
因此,在查询时需要从上至下一层层的搜索,而第一条找到的就是我们要读的结果!
LSM-Tree结构特性
LSM-Tree 的结构特性和 BTree 截然不同:
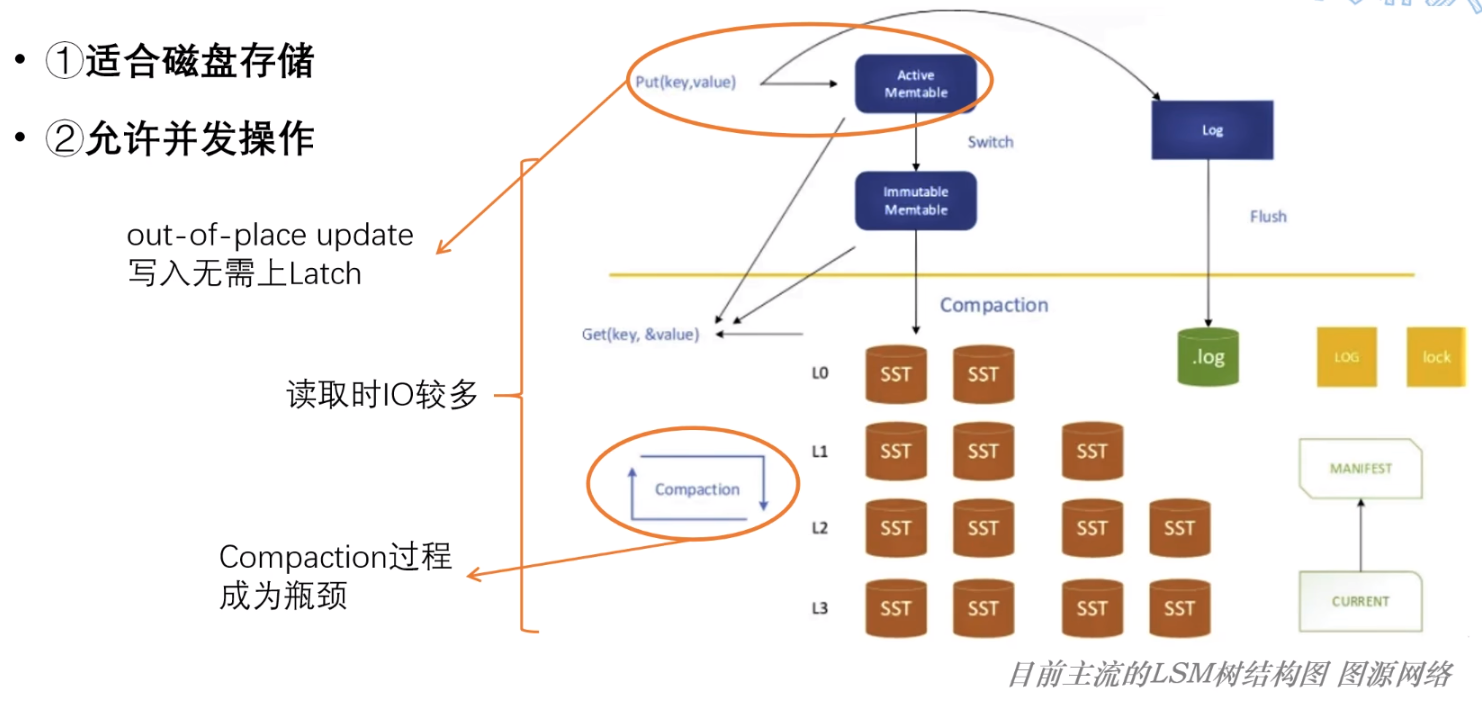
由于其 Out-of-place 的特点:所以在正常插入到内存时,完全不会改变历史数据的结构,即:没有 SMO 过程;
因此,并发能力很强,BTree 在特性2上的瓶颈在 LSM-Tree 中不存在;
而 LSM-Tree 中每层数据都比较多,在缓冲池没有命中时,读取 LSM-Tree 时读取的次数可能会非常多!
所以,LSM-Tree 在特性1上的表现并不好!
但是,可以优化 LSM-Tree 的特性1,下面是几个常用的优化手段:
- 依靠 Compaction 操作整理 LSM-Tree 的结构,减少读 IO 的次数;
- 使用 Bloom Filter 对数据进行过滤;
实际上 Compaction 操作就可以看作为 LSM-Tree 的 SMO 操作!
在 Compaction 期间,不仅会占用大量资源,并且还会造成缓冲丢失、写停顿(write stall)等问题,减少并发能力;
因此,对 LSM-Tree 优化的关键点就落在 Compaction 操作上;
In-place和Out-of-place update方案差异
对于 In-place update 结构而言:
需要把磁盘中的结构加载到内存中,再修改并写回至磁盘中,因此免不了要使用 Latch 机制来做并发控制;
而对于 Out-of-place update 结构而言:
虽然存在其他因素干扰其并发能力,但是由于所有的写入都是追加操作,因此无需采用基于 Latch 的机制进行并发控制;
由于现在多核处理器的发展,NUMA 模式逐渐成为主流,多核处理器在面对 Latch 的频繁获取和释放时都会损耗很多性能;
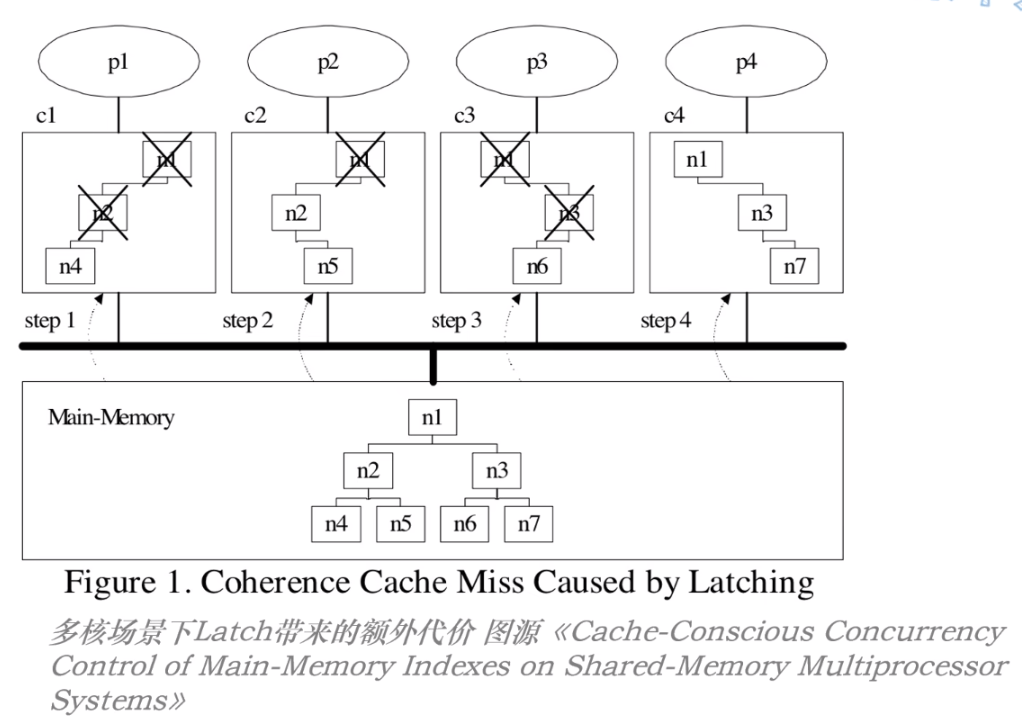
可以简单理解:
CPU 中每个核都有独立的一块存储区域,而读取或者写入的过程就需要将页数据加载到这块存储区域中;这样,并发读写时,一些节点就可能会存在多个核空间中;
而加 Latch 和解 Latch 的操作又必须同步给多个核,这就造成了很大的性能损耗;
最显著的例子,对于 B+Tree 而言,在读写时由于根节点是必经之路,因此频繁的对根节点加解 Latch 就会极大的影响多核场景下的并发性能!
NUMA:
非统一内存访问架构(英语:non-uniform memory access,简称NUMA)是一种为多处理器的电脑设计的内存架构,内存访问时间取决于内存相对于处理器的位置。在NUMA下,处理器访问它自己的本地内存的速度比非本地内存(内存位于另一个处理器,或者是处理器之间共享的内存)快一些;
深入了解BTree及其变种
下面列出了 BTree 的一些变种:
- BTree:
- B+Tree;
- B*Tree => B-Link Tree;
- CoW BTree;
- 惰性 BTree;
- Bw Tree;
另外还有一些其他变种,例如:FD-Tree;
下面具体来分析这些变种的优势和发展趋势;
下图是原始 BTree 的结构:
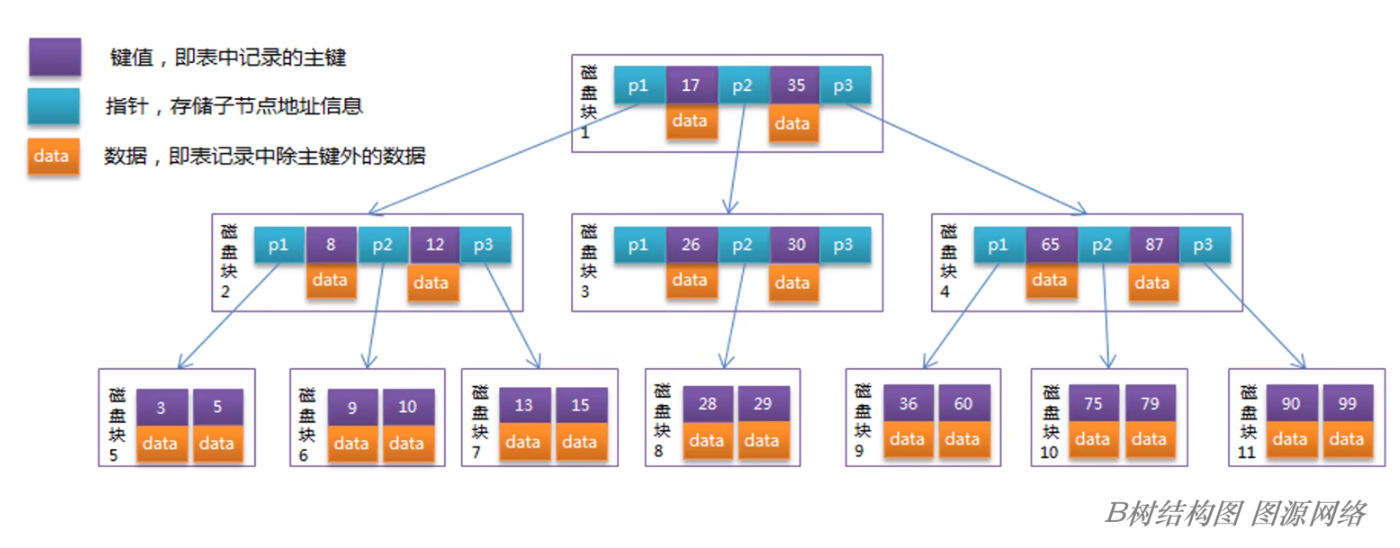
可以注意到:在 BTree 中,每个数据只存储一份;
如果要进行全表扫描,则需要中序遍历整个 BTree,因此会产生大量的随机 IO,性能不佳;所以基本上没有直接使用 BTree 实现存储结构的;
BTree 早期有两个变种:
- B+Tree;
- B*Tree
B+Tree
相比于 BTree,B+Tree 的数据按照键值大小顺序存放在同一层的叶子节点中(和上面 BTree 中在非叶子节点也存放数据不同),各个叶子节点按照指针连接,组成一个双向链表;
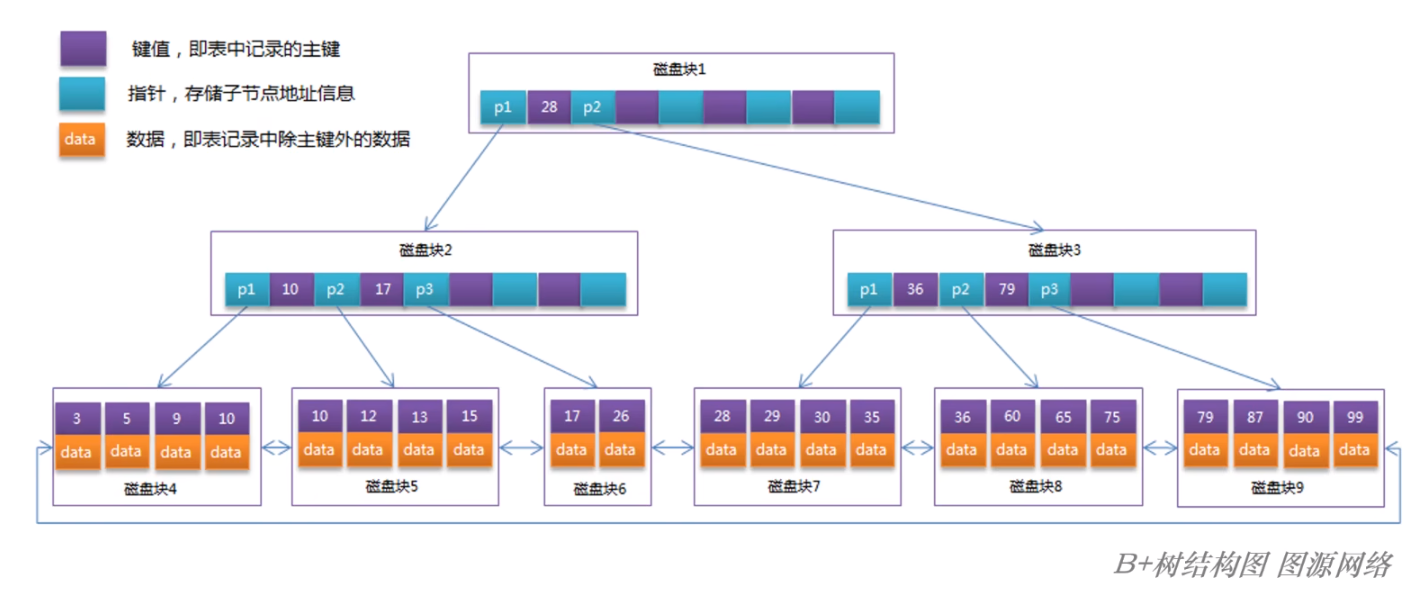
因此,对于 B+Tree 而言,其非叶子节点仅仅作为查找路径的判断依据,一个 key 值可能在 B+Tree 中存在两份(仅 Key 值)!
B+Tree 的结构解决了 BTree 中中序遍历扫描的痛点,在一定程度上也能降低层数;
B*Tree
B*Tree 是 BTree 的另一个变种,其最关键的一点是将节点的最低空间利用率从 BTree 和 B+Tree 的 1/2 提高到了 2/3,并由此改变了节点数据满时的处理逻辑;

我们知道,BTree 和 B+Tree 的空间利用率为 1/2,即:当他们的叶子节点满而分裂时,默认状态下会分裂为两个各占一半数据的节点;
而 B*Tree:在一个节点满了却又有新的数据要插入进来时,他会将其部分数据搬迁到下一个兄弟节点,直到两个节点空间都满了,就在中间生成一个节点,三个节点平分原来两个节点中的数据;
上面选取《The Ubiquitous B-Tree》论文对 B*Tree 的解释;
B*Tree 的思想主要是:将当前节点和兄弟节点相关联;
B*Tree 的这种设计虽然可以提升空间利用率,对减少层数、提升读性能有一定的帮助,但这种模式增加了写入操作的复制度;
而且向右兄弟节点搬迁数据的过程也要视作为一种 SMO 操作,对写入和并发能力有极大的损耗!
因此,B*Tree 并没有被大量使用;
B-Link Tree
由于 BTree 存在上面所述的劣势,但是基于 **将当前节点和兄弟节点相关联** 的思想,在此基础之上提出了 B-Link Tree,赋予了其突破 BTree 并发控制能力的瓶颈;
补:BTree并发机制
这里以 MySQL InnoDB 存储引擎为例,讲述基于 B+Tree 的存储引擎是如何通过 Latch 进行并发控制的;
在 MySQL 5.6 之前的版本,只有写和读两种 Latch,被称为 X Latch 和 S Latch;
MySQL 5.6 之前的版本
B+Tree并发读取
对于读的过程,首先要在整个索引上添加 Index S Latch;
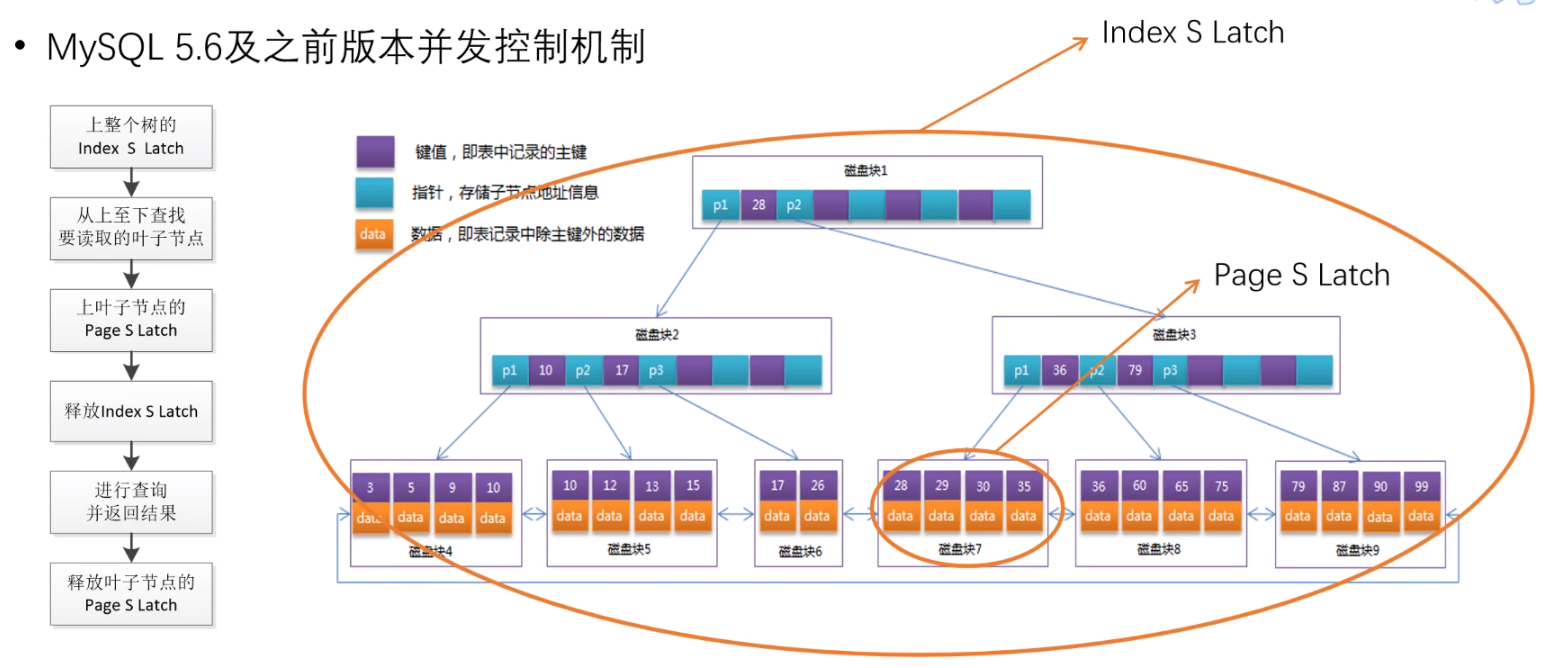
再从上至下找到要读的叶子节点的 Page,然后上叶子节点的 Page S Latch;
这时就可以释放 Index S Latch了;
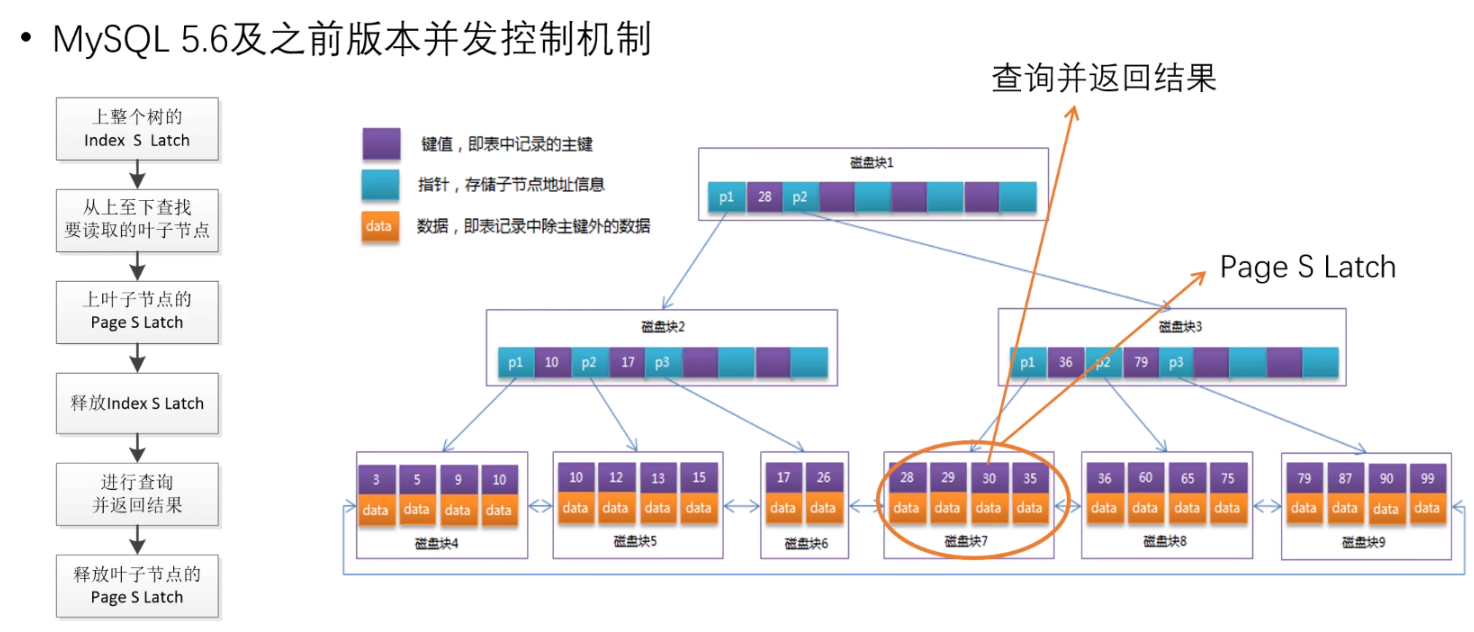
然后进行查询并返回结果,最后释放叶子节点中的 Page S Latch,完成整个读操作;
B+Tree乐观写
写的过程就有些复杂了;
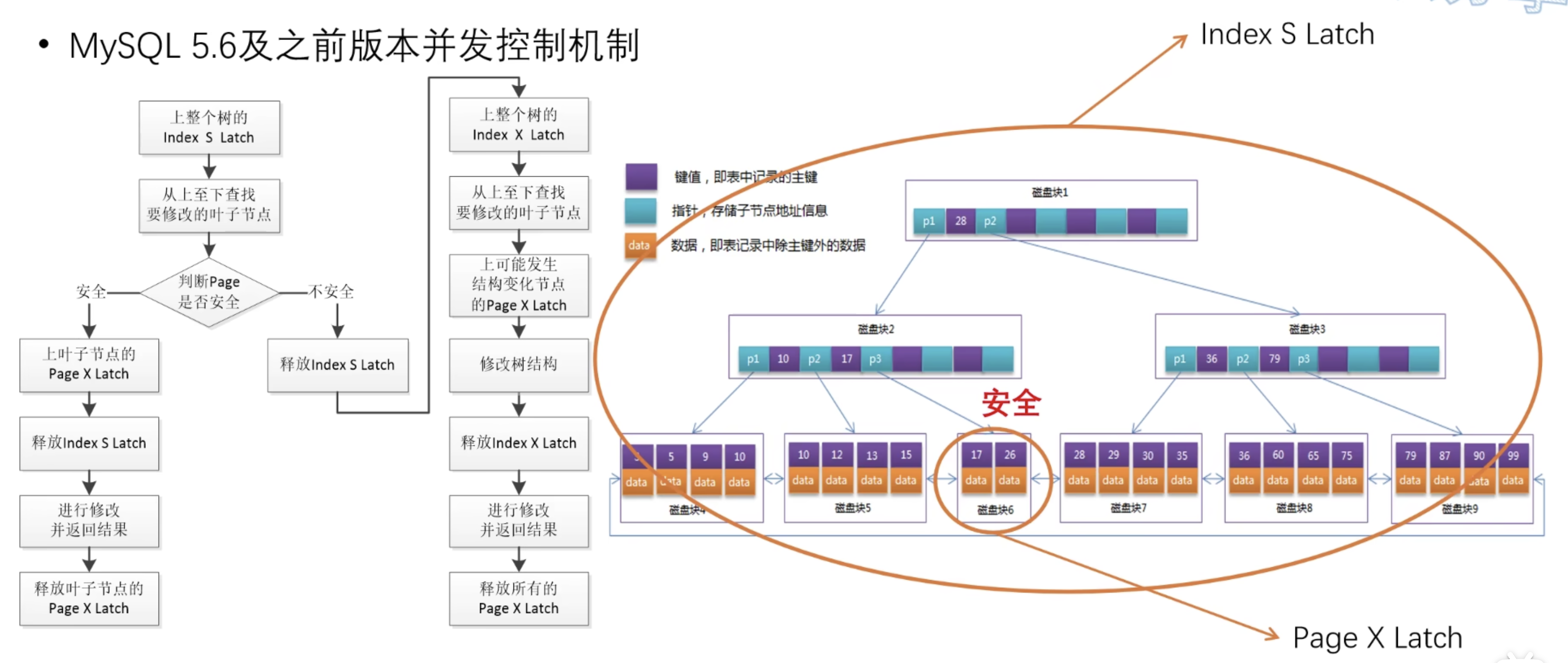
首先进行乐观的写入,即:假设写入操作不会引起索引结构的变更(不触发 SMO 操作);
要先上整个索引的 Index S Latch,再从上至下找到要修改的叶子节点的 Page,此过程和上面的读取步骤相同!
接下来判断叶子节点是否安全,即:写入操作是否会触发分裂或者合并;
如果叶子节点 Page 安全,就上 Page X Latch,并释放 Index S Latch,然后再修改数据即可;
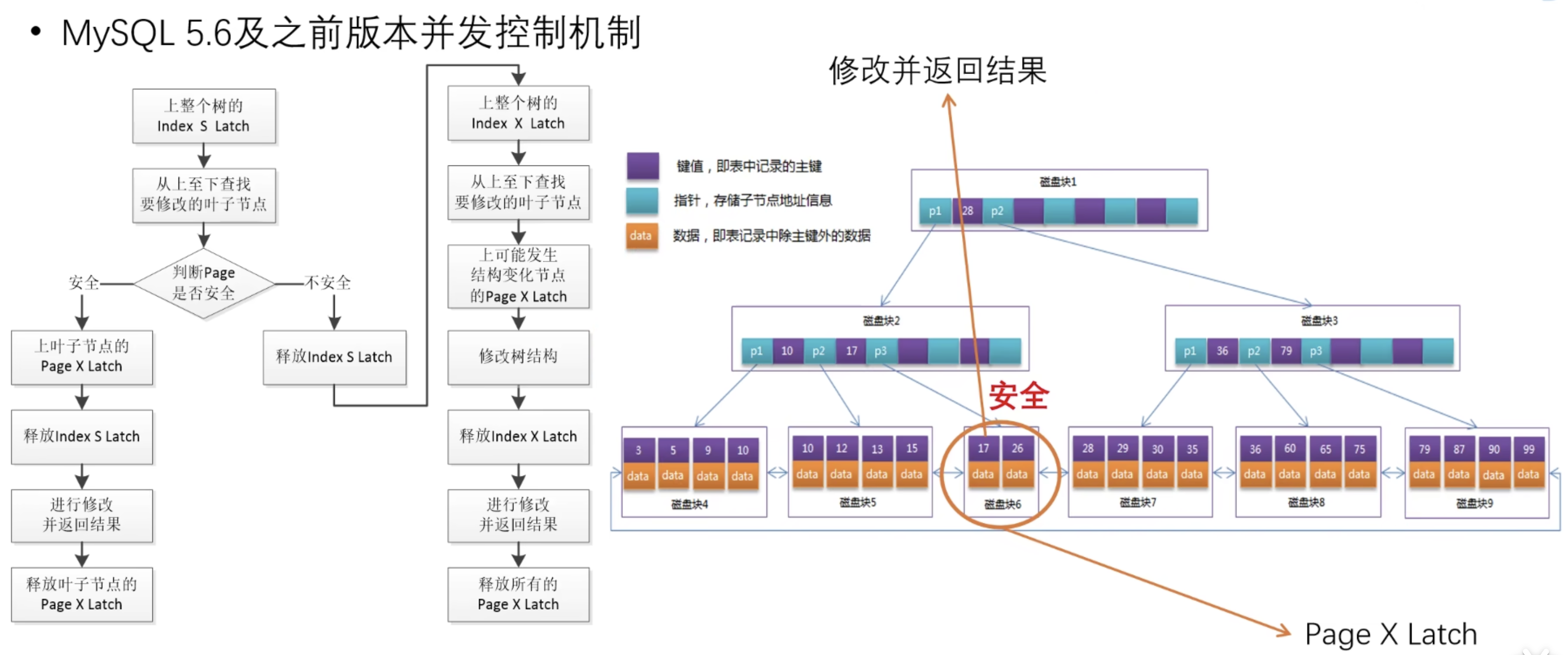
上面就完成了乐观写入的过程;
B+Tree SMO悲观写入
如果叶子节点 Page 不安全,那么就要重新进行悲观写入;
释放一开始上的 Index S Latch,重新上 Index X Latch,阻塞对整颗 B+Tree 的所有操作;
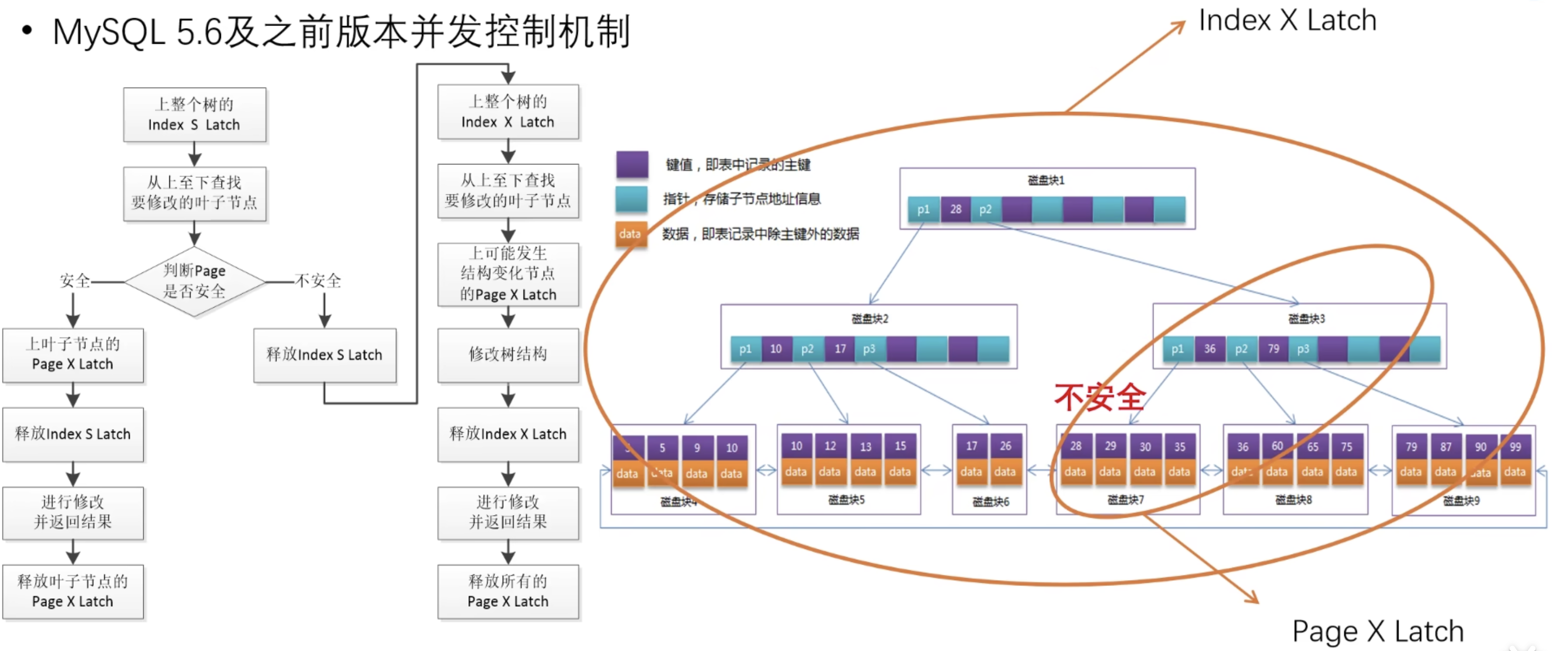
然后重新搜索,并找到要发生结构变化的节点,上 Page X Latch,再修改树结构,此时可以释放 Index X Latch;
完成悲观写入过程;
上 Index X Latch 的原因是:
有可能 SMO 操作会逐级向上传递,直到根节点!
MySQL 5.7之后的版本
从前面的分析可以看出来,上面加锁的缺点非常明显:
在触发 SMO 操作过程时,由于会持有 Index X Latch 锁住整棵树;此时所有操作都无法进行,包括读操作;
因此,在 MySQL 5.7、8.0 版本中,针对 SMO 操作会阻塞读的问题,引入了 SX Latch;
SX Latch 介于 S Latch 和 X Latch 之间,和 X Latch、SX Latch 冲突,但是和 S Latch 不冲突(可以理解为类似RWLock);
| S Latch | SX Latch | X Latch | |
|---|---|---|---|
| S Latch | 兼容 | 兼容 | 不兼容 |
| SX Latch | 兼容 | 不兼容 | 不兼容 |
| X Latch | 不兼容 | 不兼容 | 不兼容 |
下面来看一下引入 SX Latch 之后的并发控制方案;
B+Tree并发读取
对于读操作而言:
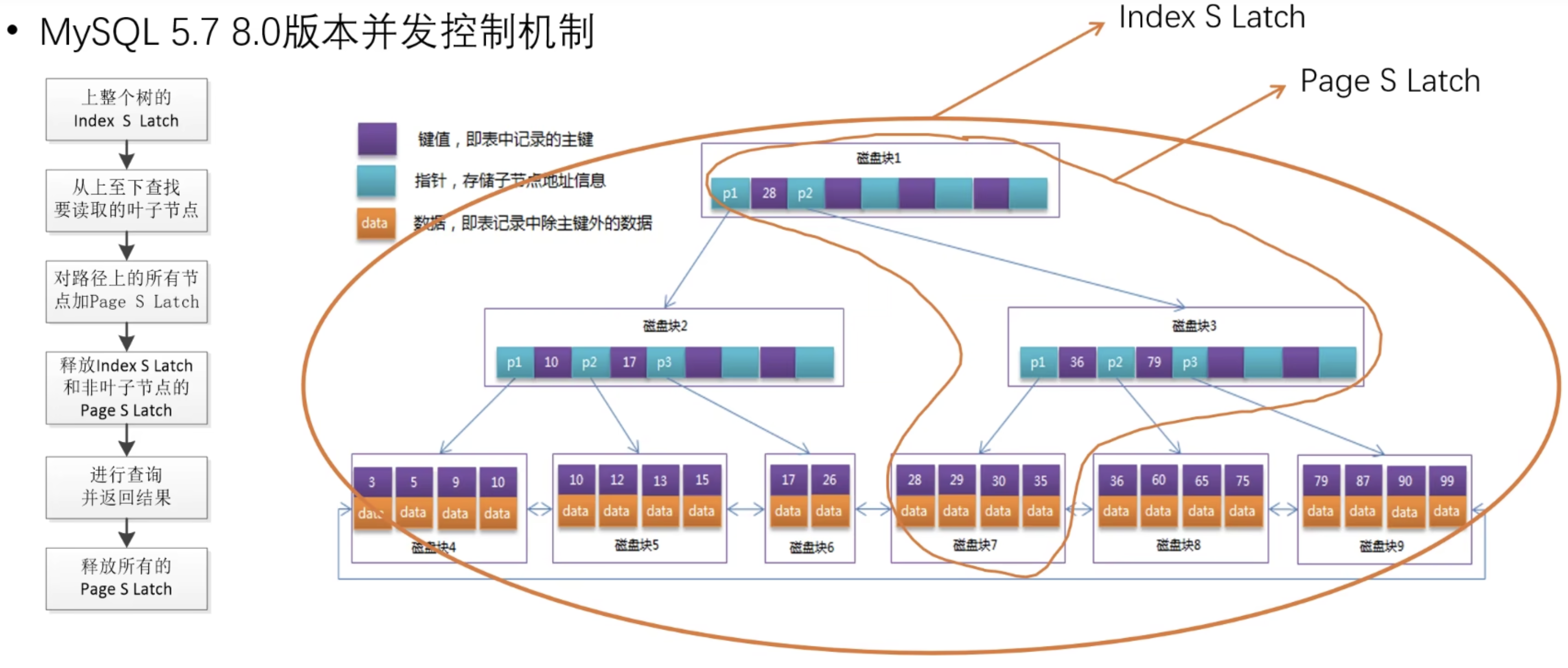
对于读操作而言:
相比于 MySQL 5.6 之前,这时读步骤主要加上了对查找路径上节点的锁;
这时因为:
在引入了 SX Latch 之后,发生 SMO 操作的时候,读操作也可以进行;
此时为了保证读取的时候查找路径上的非叶子节点不会被 SMO 操作改变,因此就需要对路径上的节点也加上 S Latch;
主要注意的是:
Index 级别和 Page 级别是两种不同对象的 Latch,因此哪怕有 Index 上的 X Latch 或者 SX Latch,也不会阻塞 Page 上的 S Latch!
B+Tree乐观写
写的过程和上面类似,一样是先进行乐观写;
由于此时假设只会修改叶子节点,因此,乐观写的查找过程和读操作一致:
添加整个索引的 Index S Latch 和读取路径上节点的 Page S Latch 即可!
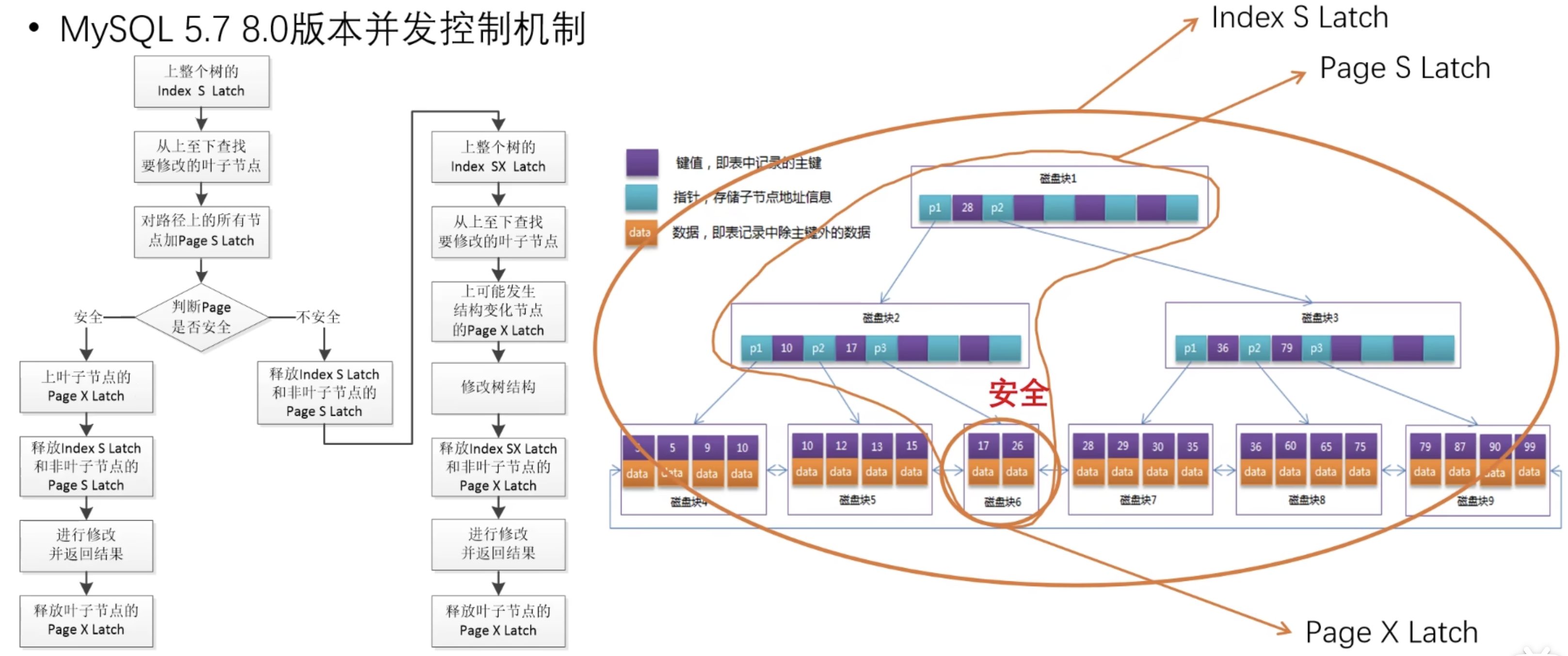
接下来判断叶子节点是否安全,如果叶子节点 Page 安全,则上 Page X Latch,同时释放索引和路径上的 S Latch;
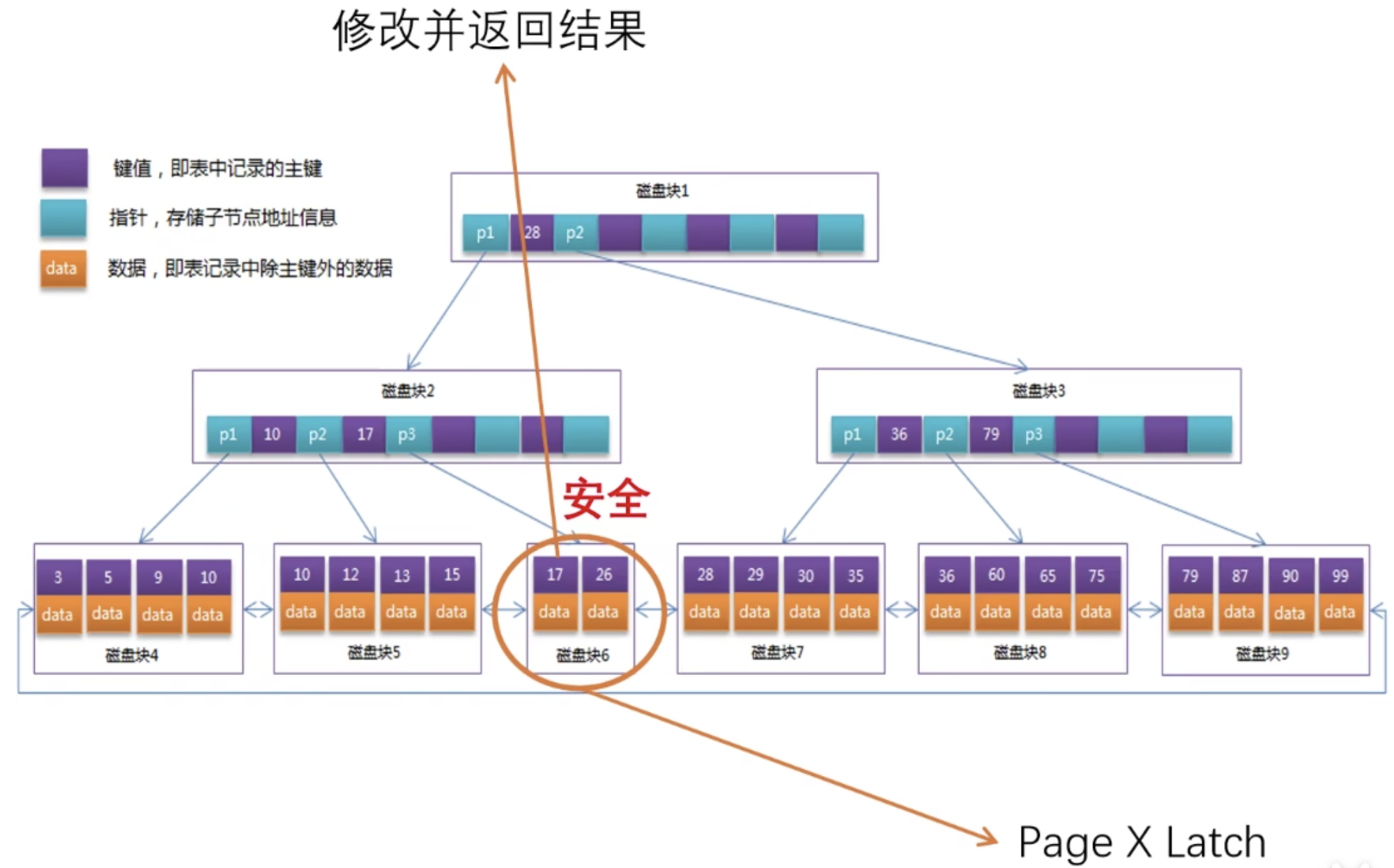
然后再修改即可;
B+Tree悲观写
但是如果叶子节点的 Page 不安全,这需要重新进行悲观写入;
释放一开始上的所有 S Latch,这时我们上 Index SX Latch,然后重新搜索,找到要发生结构变化的节点;
上 Page X Latch,再修改树结构,此时就可以释放 Index SX Latch 和路径上的 Page X Latch;
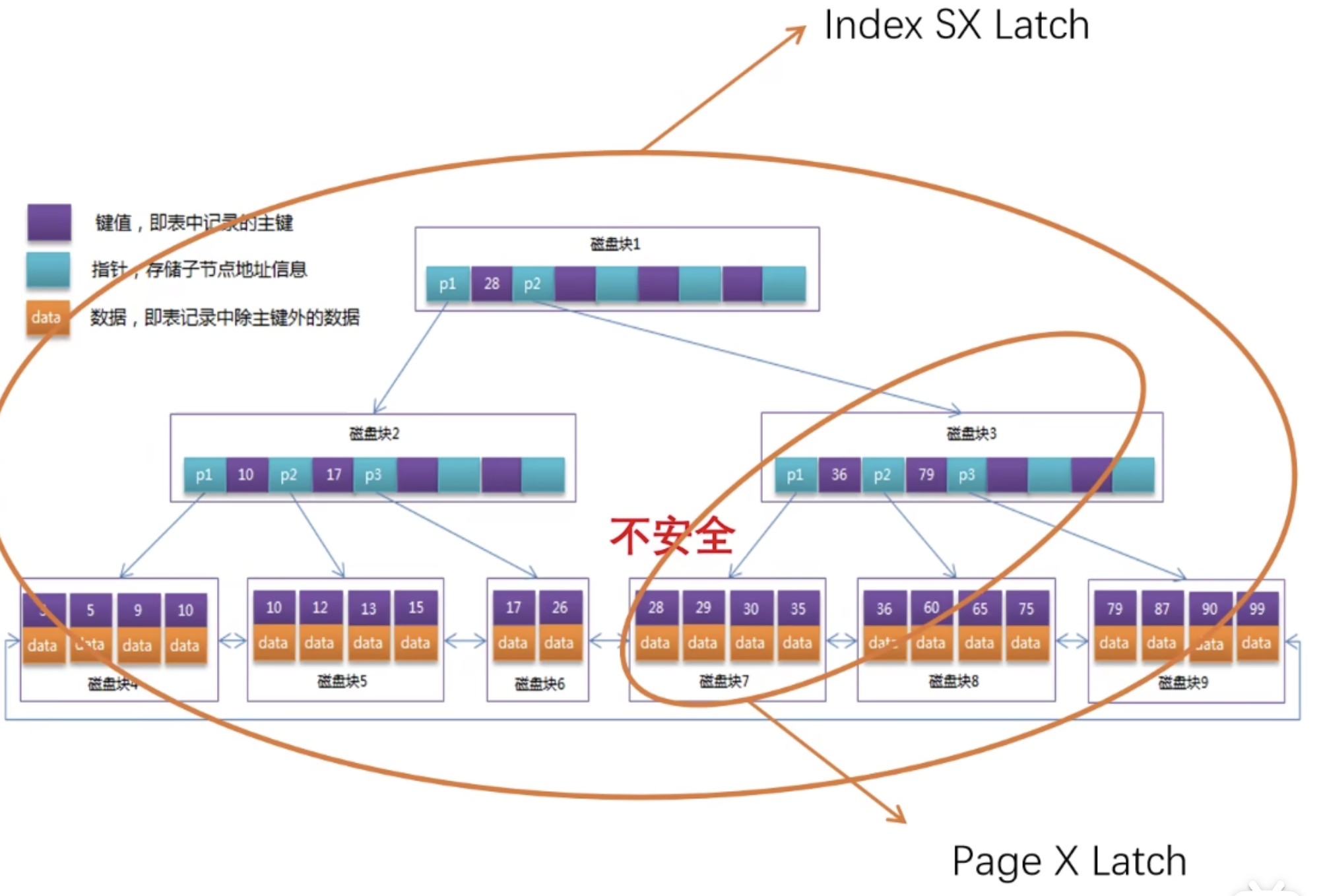
随后即可完成对叶子节点的修改,返回结果,并释放叶子节点的 Page X Latch;
最终完成悲观写入!
上面就是 MySQL 对 B+Tree 并发控制机制的发展;
当然,对 B+Tree 并发控制的研究和方案原因不止上面介绍的内容,这里只是为了说明 B+Tree 并发控制的痛点;
B-Link Tree并发控制优化
补充了上面的内容,我们可以知道,B+Tree 的问题在于:
其自上而下的搜索过程决定了加锁过程也必须是自上而下的!
哪怕只对一个小小的叶子节点做读写操作,也都必须首先对根节点上 Latch!
并且,一旦触发 SMO 操作,就需要对整个树进行加锁!
B-Link Tree 相比于 B+Tree 主要做了三点优化:
- 1、非叶子节点也都有指向右兄弟节点的指针;
- 2、分裂模式上,采用和 BTree 类似的做法,即:*将当前层数据向兄弟节点中迁移;**
- 3、每个节点都增加一个 High Key 值,记录当前节点的最大 Key;
B-Link Tree 结构如下图:
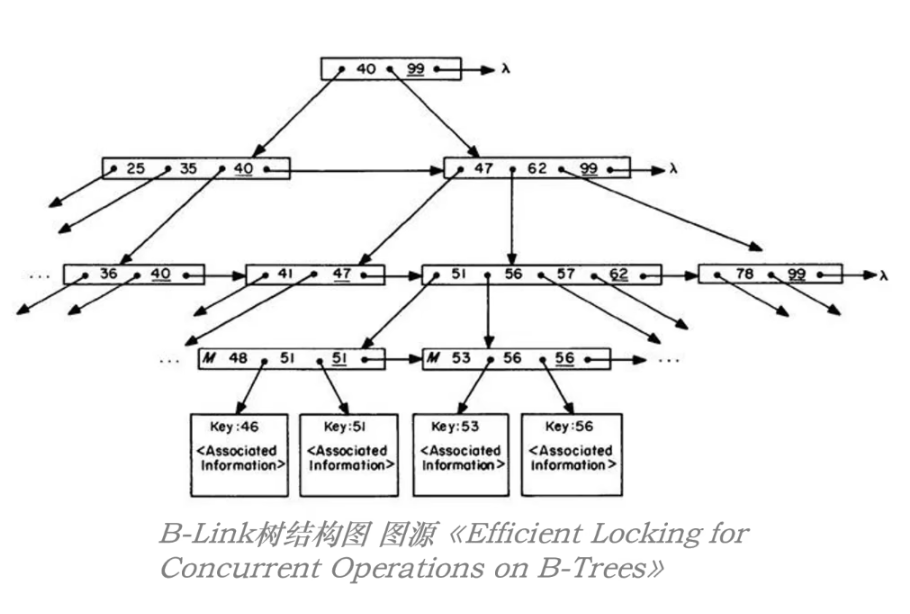
其中加下划线的 Key 为 High Key;
在前面提到,B+Tree 中一个严重的问题就是,在读写过程中都需要对整棵树、或一层层向下的加 Latch,从而造成 SMO 操作会阻塞其他操作;
而 B-Link Tree 通过对分裂和查找过程的调整,避免了这一点!
下图就是 B-Link Tree 树节点分裂的过程;
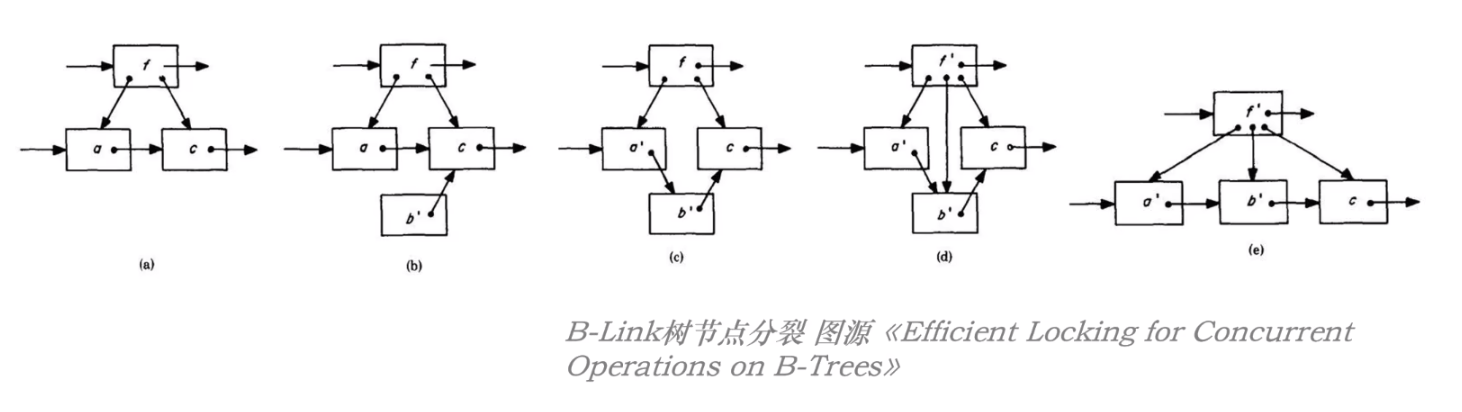
可以看到,上面的操作继承了 B*Tree 的思路:
先将老节点的数据拷贝到新节点,然后建立同一层节点的连接关系,最后再建立从父节点指向新节点的连接关系(此顺序非常重要!);
那么上面的分裂过程是如何避免整棵树上的锁的呢?
可以通过指向右兄弟节点的指针和 High Key 实现!
如下图,当节点 y 分裂为 y 和 y+ 两个节点后,在 B+Tree 中就必须要提前锁住他们的父节点 x;
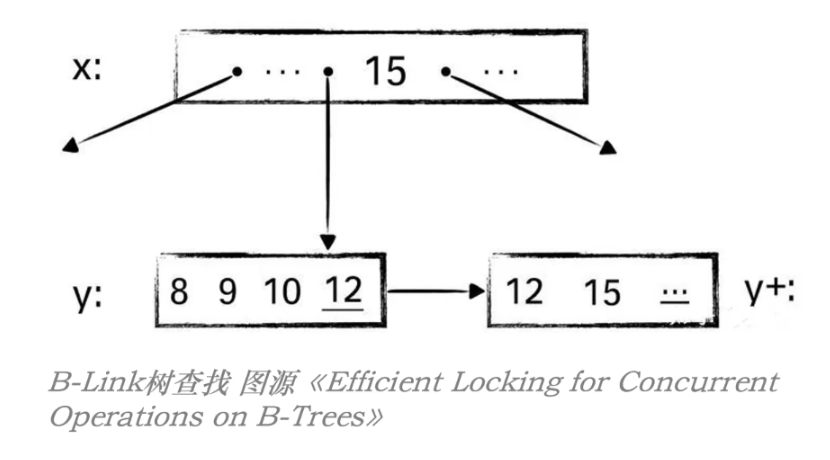
而 B-Link Tree 可以先不锁 x,这时查找 15,顺着 x 找到节点 y,在节点 y 中未能找到 15,但判断 15 大于其中记录的 high key,于是顺着指针就可以找到其右兄弟节点 y+,仍能找到正确的结果;
因此,B-Link Tree 中的 SMO 操作可以自底向上加锁,而不必像 B+Tree 那样自顶向下加锁!从而避免了 B+Tree 中并发控制瓶颈;
上面就是 B-Link Tree 的基本思路;
但是在实现 B-Link Tree 时需要考虑的还有很多:
- 删除操作需要单独设计;
- 原论文中对于一些原子化的假定也不符合现状;
但是 B-Link Tree 仍是一种非常优秀的存储结构,很大程度上突破了 B+Tree 的性能瓶颈;
PostgreSQL 的 BTree 类型索引就是基于 B-Link Tree 实现的!
下面再来看一看最近比较新的一些 BTree 变种,这些变种很大程度上都采用了和 LSM Tree 类似的思想;
CoW BTree
CoW BTree 也称写时复制 BTree,CoW BTree 采用 Copy-on-Write 技术来保证并发操作时的数据完整性,从而避免使用 Latch;
写入时复制(英语:Copy-on-write,简称COW)是一种计算机程序设计领域的优化策略;
其核心思想是:
如果有多个调用者(callers)同时请求相同资源(如内存或磁盘上的数据存储),他们会共同获取相同的指针指向相同的资源,直到某个调用者试图修改资源的内容时,系统才会真正复制一份专用副本(private copy)给该调用者,而其他调用者所见到的最初的资源仍然保持不变,这过程对其他的调用者都是透明的(transparently);
此作法主要的优点是如果调用者没有修改该资源,就不会有副本(private copy)被建立,因此多个调用者只是读取操作时可以共享同一份资源;
当某个页要被修改时,就先复制整个页的内容,然后在复制出来的页上进行修改;
当然,复制产生的新页要替换旧页,此时父节点指向这个页的指针就要变化了;CoW BTree 的做法也非常的粗暴:
直接将父节点也复制并修改一份!
接下来再复制并修改父节点的父节点,直到根节点!
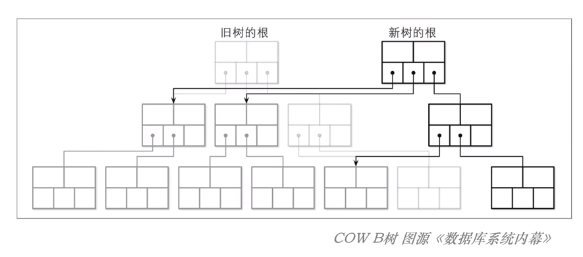
CoW BTree 的修改逻辑如上图所示:
对于叶子节点的修改会产生一个全新的根节点(即:一个全新的树)!
CoW BTree 在很大程度上具有 Out-of-place update 的特性,因为已经写入的页是不变的,所以 CoW BTree 可以像 LSM Tree 那样,完全不依赖 Latch 实现并发控制!
但是,为了达成这一点,CoW BTree 付出的代价也是非常巨大的:为了修改一个小小的数据,就要重新复制多个页,带来巨大的写放大!
也正是因为上面的问题,因此 CoW BTree 也一直没能成为主流;
但是 CoW BTree 的思路却很重要!后续的许多变种都对其进行了借鉴和改良;
Lazy BTree(惰性BTree)
惰性 BTree 相比于上面提到的 CoW BTree 更进一步,为每个页都设置了一个更新缓冲区;
这样,更新的内容就放在了更新缓冲区中;
读取时,将原始页中的内容和更新缓冲区进行合并,来返回正确的数据;
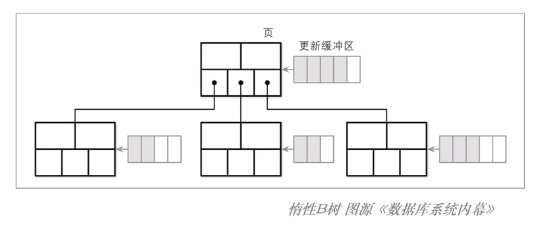
惰性 BTree 和 LSM Tree 极为相似,甚至可以说,惰性 BTree 中的每一个页就像一个小型的 LSM Tree!
而更新缓冲区就像 MemTable,当更新缓冲区达到一定程度,就压缩到页中,类似于一个小的 Compaction 的过程!
惰性 BTree 同样避免了 Latch 机制,同时没有 CoW BTree 那么大的写放大代价,因此具有良好的性能;
MongoDB 的默认存储引擎 WiredTiger就是使用的这种存储结构!
Lazy-Adaptive Tree(惰性自适应BTree)
惰性 BTree 还有一个分支:Lazy-Adaptive Tree(LA Tree);
整体思路和 Lazy BTree 一致,只是将更新缓冲区中的对象变为子树,用来进一步减少写放大;
如下图所示:
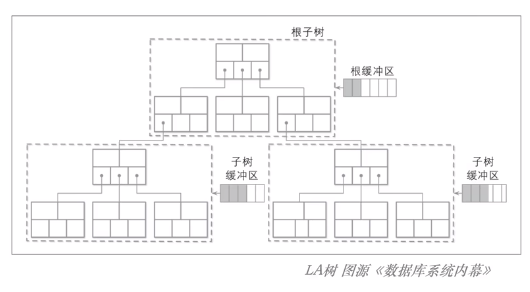
Bw Tree
随着新硬件(如:SSD存储)技术的发展,其硬件实现原来越有利于 LSM Tree;
因此,BTree 方面自然也会对新硬件做出适应性的改造,如:CoW BTree 和 Lazy BTree,都在相当程度上具有和 LSM Tree 类似的特性了;
本小节所介绍的 BwTree 是在这一方向上更进一步的一种 BTree 变种,甚至在很大程度上比 LSM Tree 都更近了一步!

BwTree 整体分为三层,从上而下分别是:
- BwTree 索引层;
- 缓冲层;
- 存储层;
对于最上层的 BwTree 索引层,可以理解为一个逻辑上的类 BTree 结构,对外提供操作这个索引结构的 API,但其实现是完全无 Latch 的;
最底层的 Flash Layer 使用了 Log Structure Store 来与固态硬盘交互,管理物理数据结构;
Log Structure Store:
利用 Append,即日志追加形式来实现的文件系统;其更符合 SSD 特性;
原理类似于 LSM Tree;
对于缓冲层,他将索引层和存储层连接起来,通过一个映射表 Mapping Table,记录逻辑页号到物理指针的映射,来实现了无锁追加的特性;
来看下面的例子;
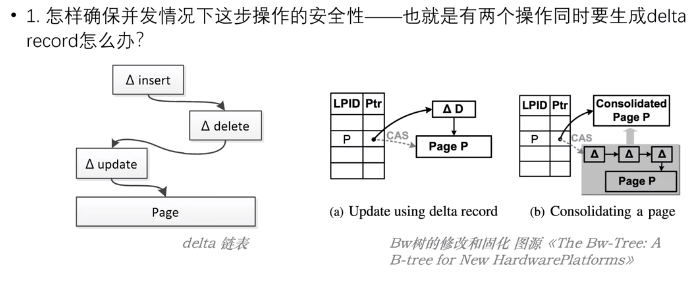
和 Lazy BTree 类似,BwTree 对每个节点的修改也是不直接修改页,而是生成一个 Delta Record 的结构,记录本次修改的情况,如果再有修改就再生成一个;
因此,许多个 Delta Record 和页一起,组成了一个类似链表的数据结构(Delta 链表);
在查找时:
从新 Delta Record 向旧 Delta Record 至数据页查找,找到符合条件的结果就返回;
这里和 LSM Tree 的查找过程非常类似!
但是这里存在两个问题:
- 如何确保并发情况下,生成 Delta Record 的安全性(两个操作要同时生成 Delta Record);
- 发生数据结构的修改,如:分裂、合并节点如何操作;
并发情况下,生成 Delta Record
对于第一个问题,BwTree 通过刚刚所说的映射表 Mapping Table,记录从逻辑页号到 Delta 链表头的指针;
如果要新增 Delta Record 就要修改 Mapping Table 中的 Value;
这样,BwTree 将修改 Delta Record 的操作,转变为了修改 Mapping Table 的操作,再通过 CAS 操作实现对 Mapping Table 的修改,从而将整个过程原子化,以实现不依赖 Latch 的并发控制;
CAS操作:
直接修改值的 CPU 指令,是一个CPU层面的原子指令;
因此,调整 Delta 链表的操作就变得简单了:
如果要修改一页中某一行的值,首先生成 Delta Record 结构,为其赋值,并让他指向原 Delta 链表头;
随后,在 Mapping Table 中通过 CAS 操作将页号映射至这个 Delta Record;
这样,整个修改操作就完成了!
如上图(a);
如果 Delta 链表过长,则需要将他们固化到页中,操作也大同小异:
首先生成一个新的页,将 Delta 链表加上原有 Page 中的所有结果合并到新的页中;
随后在 Mapping Table 中通过 CAS 操作将页号映射到这个新页即可!
如上图(b);
生成的新页不需要修改原来其父节点指向它的指针吗?
实际上,BwTree 中的指针可以是逻辑指针:父节点记录子节点的逻辑页号,就可以找到子节点了!
因此,只要不修改页号,父节点就不用改变;
所以,虽然我们替换了页,但是由于有映射表的存在,逻辑页号并没有变化,所以父节点也不用变化;
树结构修改
页分裂操作
当新增或删减节点时,BwTree 的做法基本上借鉴了 B-Link Tree 的思路:
采用了一个指向右兄弟节点的指针,来使分裂过程分为 child split 和 parent update 两个步骤,每个步骤都是原子操作,从而实现了原子化的 SMO 操作;
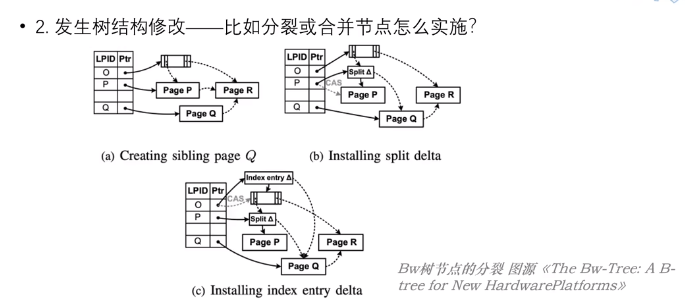
上图就是页 P 分裂为 P 和 Q 的过程;
首先(a)步生成页 Q,但这时页 P 仍然是指向原下一个节点 R 的,页 Q 不可达;
(b)步对页 P 增加了一个特殊的 Delta Record,它负责对页 P 和页 Q 两部分的数据进行路由;
(c)步再按照相似的方法调整父节点;
随着页 P 和父节点的压缩操作,会将 Delta Record 链表合并到页中!
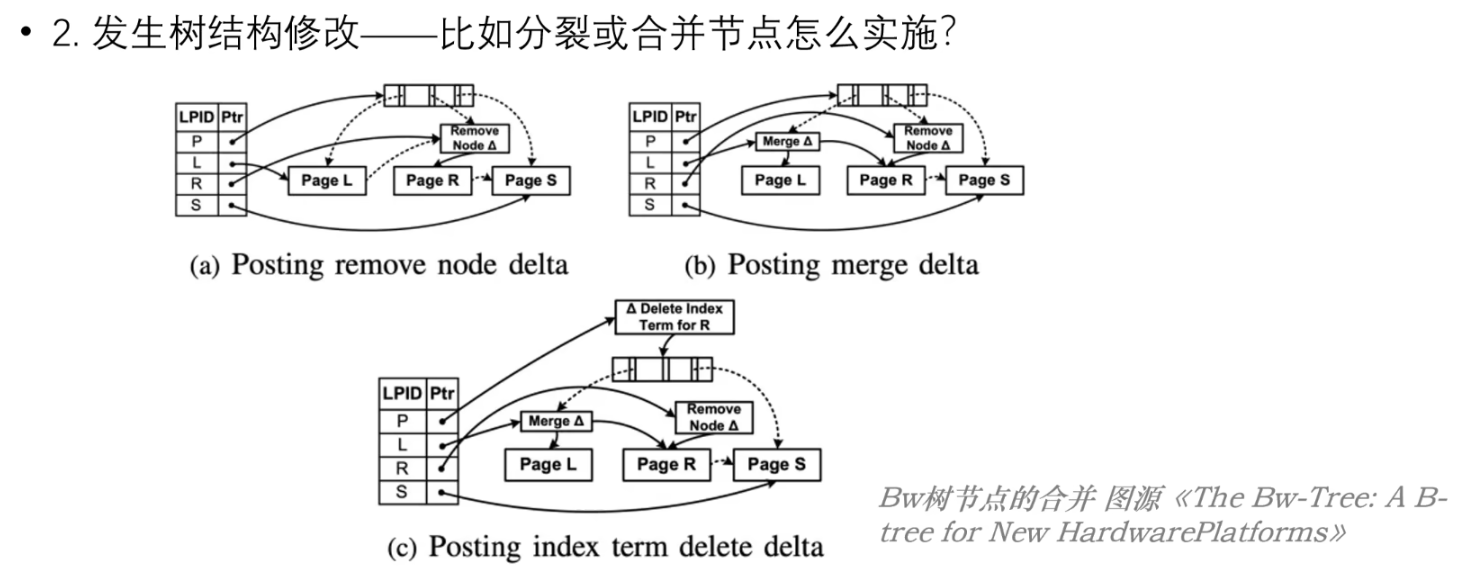
页合并操作
页合并操作和上面的分裂思路类似,先通过增加一个 remove delta record 来标记要删除的节点;
再通过对其前置节点增加一个 merge delta 标记修改,最后再修改父节点;
BwTree总结
从前面的分析可以看到,BwTree 更像是 B-Link Tree 和 LSM Tree 的结合,从而兼具无 Latch 的特性,又在相当程度上拥有 BTree 一族的读优势!
目前,BwTree 在学术界还有不少的探索和关注,但在工业界还未听说有成功的实践;
深入了解LSM-Tree及其变种
LSM-Tree概念
LSM Tree 的概念起源于 1996年的论文《The Log Structure Merge Tree》,此后由 Google Bigtable 第一个商业化实现并于 2006 年发表论文《Bigtable:A distributed strorage system for structured data》;
随后,Google 的两位专家基于 BigTable 的经验实现了 LevelDB,一个单机 LSM Tree 存储引擎,并开源;
Chrome 浏览器中的 IndexedDB 底层实现就是 LevelDB!
此后,FaceBook 基于 LevelDB 开发了 RocksDB(非常棒的 KV 数据库,非常值得学习!)!
RocksDB 做了相当多的迭代演进,如:多线程、Column Family(类似于关系型数据库中表的概念)、Compaction策略等;
目前,RocksDB 已经成为 LSM Tree 领域的一个事实标准!
包括 TiDB 底层的存储也是使用的RocksDB!
下图为 RocksDB 的结构图;
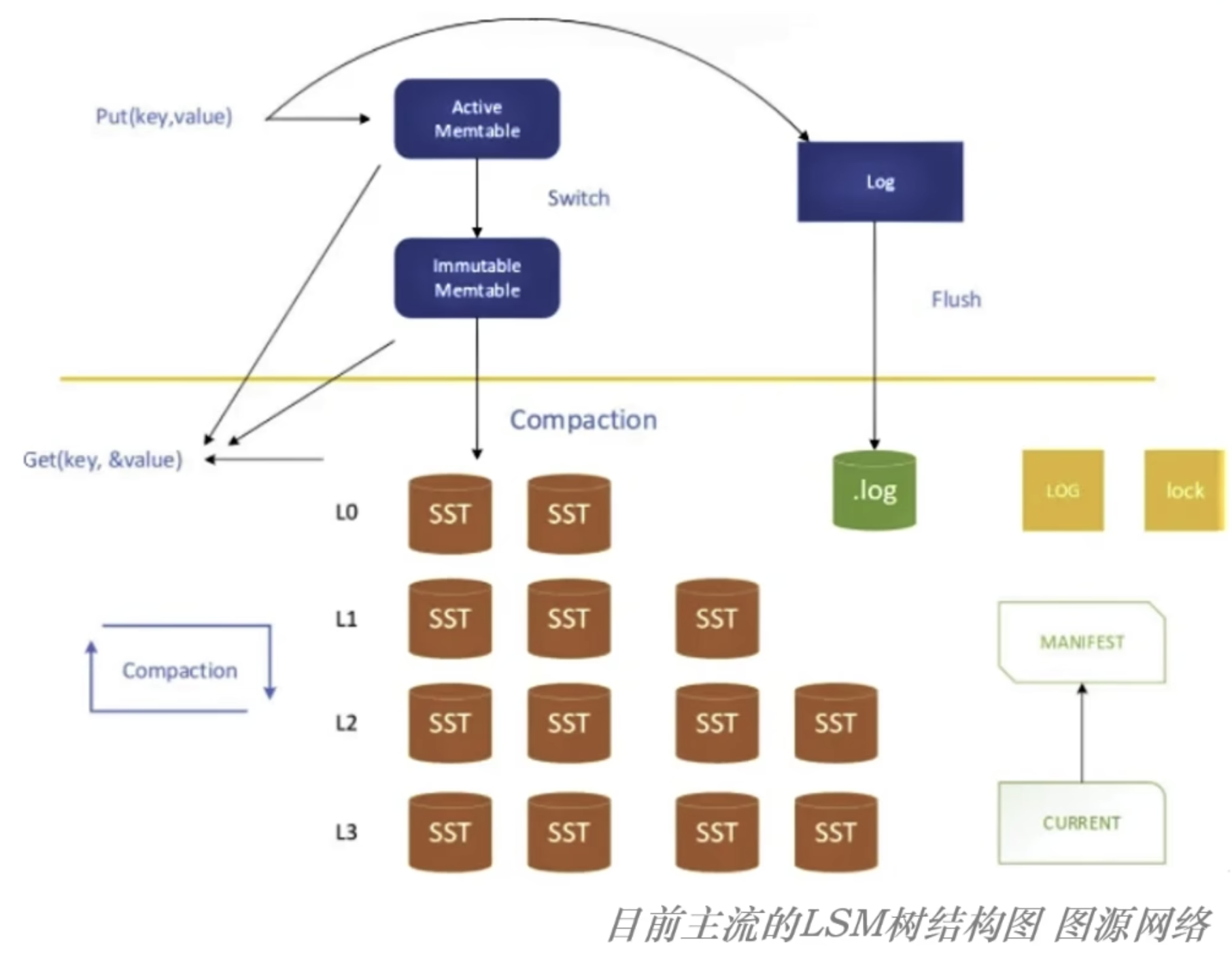
写入的数据首先要记录 WAL(Write-ahead Log),用来做实时落盘,以实现持久性;
随后,数据有序的写入 Active Memtable 中;同时,Active Memtable 也是这里唯一可变的结构!
在一个 Active Memtable 写满后,就把它转换为 Immutable Memtable;
上面两类 Memtable 都在内存中,使用的数据结构基本上是跳跃表(也有vector、hash-skiplist等)
Minor Merge
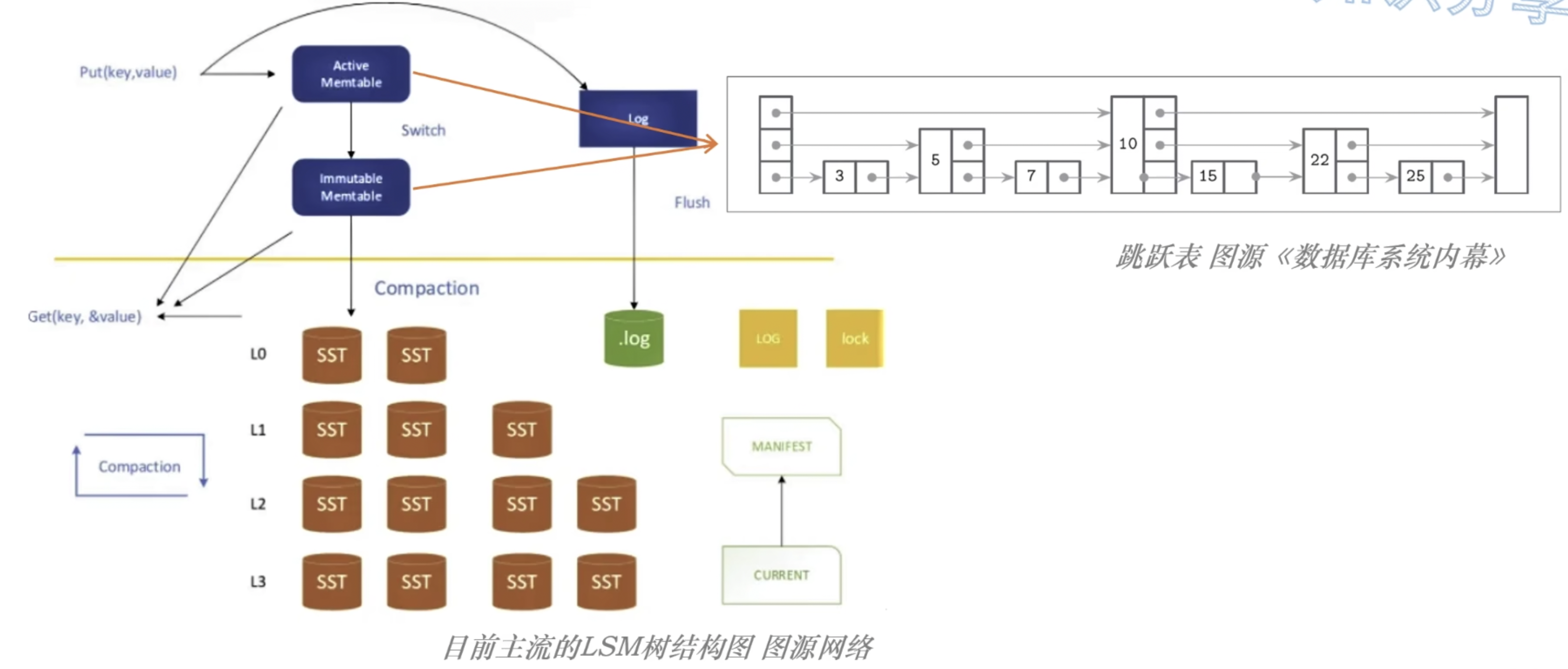
当 Immutable Memtable 达到指定的数量后,就将 Immutable Memtable 落盘到磁盘中的 L0 层;
上面这步操作被称为 minor merge;
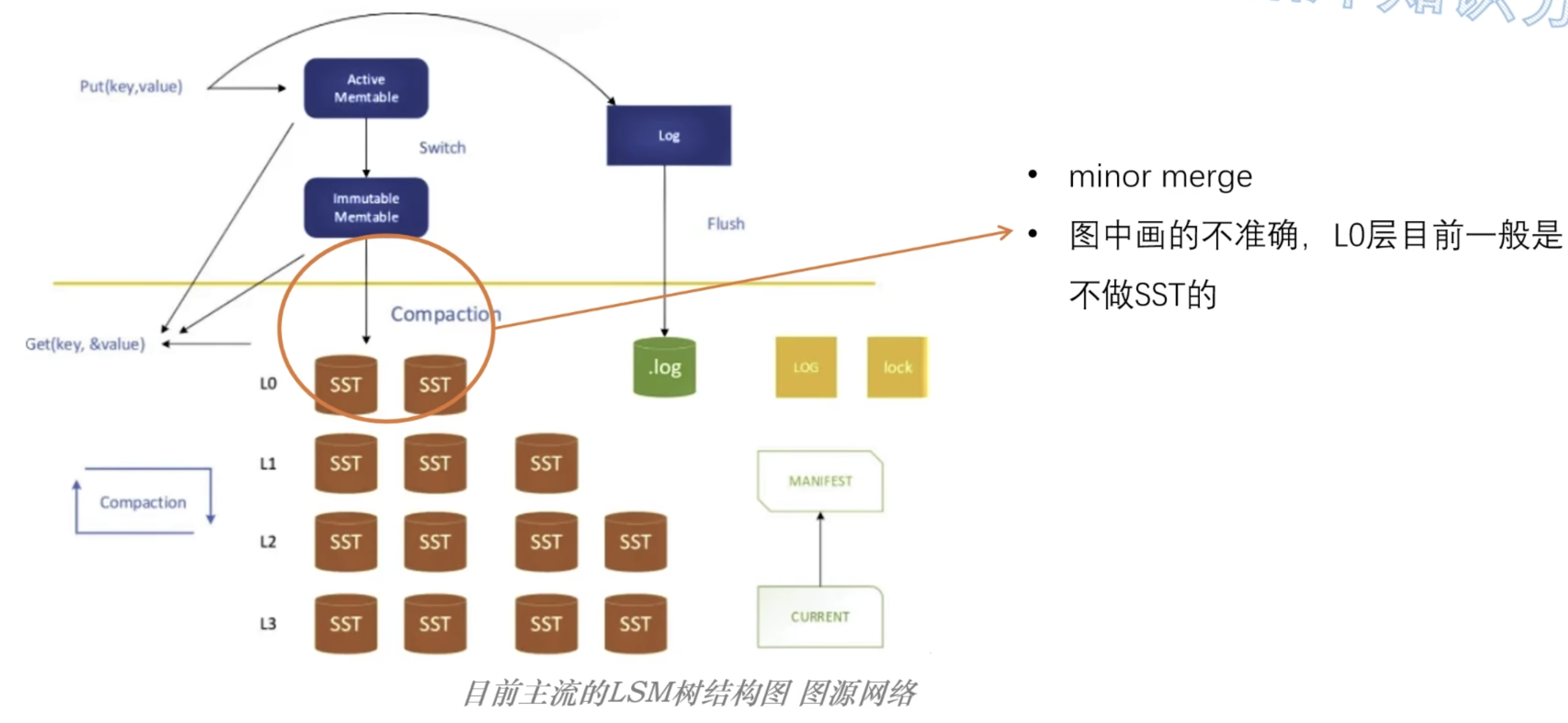
通常,对于 minor merge 的 Memtable 不做整理(无 Compaction 过程),直接刷入磁盘;
因此,L0 层可能会存在重复的数据;
Major Merge
当 L0 层的数据满了之后,就会触发 major merge,也就是关键的 Compaction 操作;
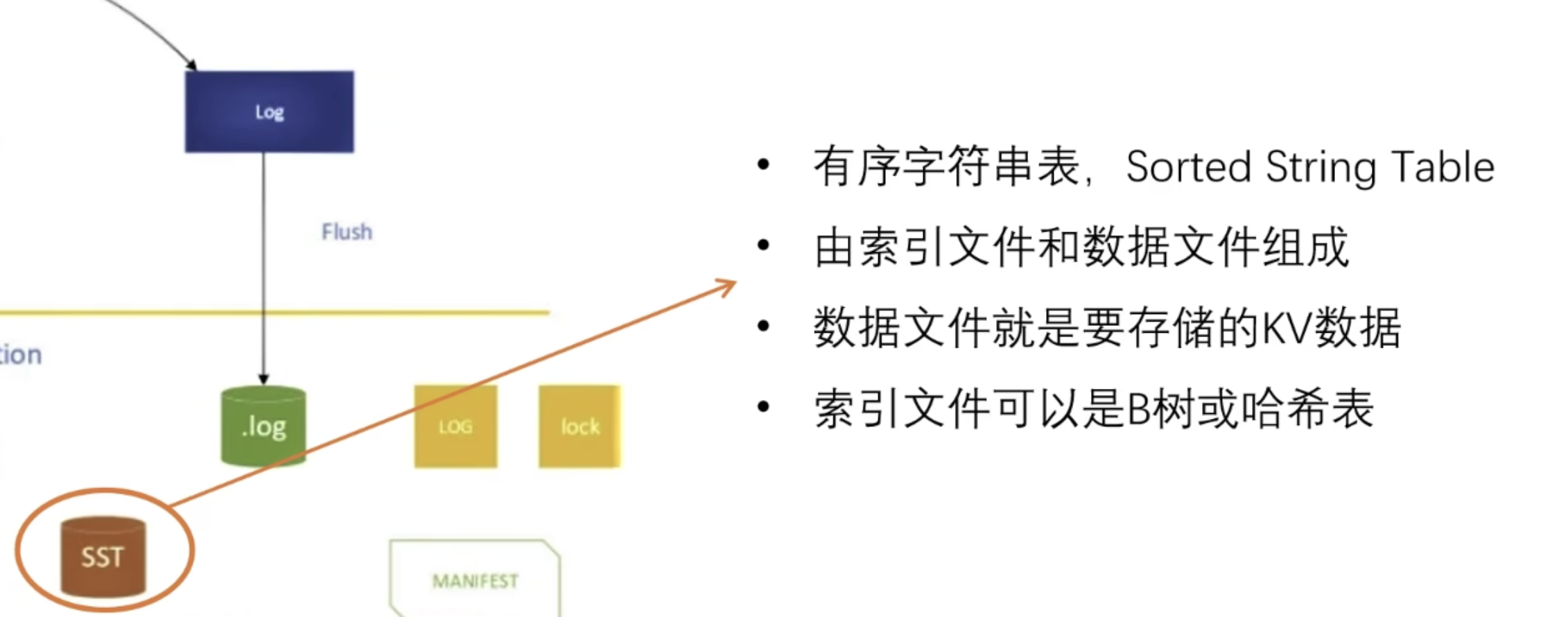
将 L0 层的数据和 L1 层的数据进行合并,全部整理为 “固定大小的、不可变的数据块”,称为 SSTable(Sorted String Table),并放在 L1 层;
SSTable 是由 LevelDB 最初实现的一种数据格式,被称为 Sorted String Table(有序字符串表);
一个 SST 通常由两个部分组成:
- 索引文件;
- 数据文件;
其中,数据文件就是要存储的 KV 数据,而索引文件可以是 BTree 或者哈希表;
(可以将 SST 理解为一个小型的聚簇索引结构,只是这个结构整体是不可变的!)
这样,除了 L0 层之外的磁盘中的每一层都是由一个个 SST 组成的,这些 SST 之间互不重叠!
SST 的出现结合后文会讲到的的 Bloom Filter,在很大程度上提升了 LSM Tree 的读性能!
并且,L1 和之后层次间的合并,可以仅合并部分重叠的 SST,使 Compaction 过程更加灵活、效率更高;
一条数据的整体写入过程
因此,一条数据进入到 LSM Tree 后会:
首先写入 active memtable,然后进入 immutable memtable,接下来被刷入 L0 层,然后随着 Compaction 操作一层层向下;
这也是 LevelDB 的由来,一层一层的;
这个过程如果碰到了更下层的同 key 数据,那么就会将对方合并;
如果在 Compaction 过程中遇到了从更高层来的同 key 新的数据,那么就会被合并;
读操作(Bloom Filter优化)
从 LSM Tree 中读取的过程就是从上至下层层扫描,直至找到数据;
在查找的过程中,有一个非常关键的优化,可以加速我们对数据的筛选,那就是:Bloom Filter!
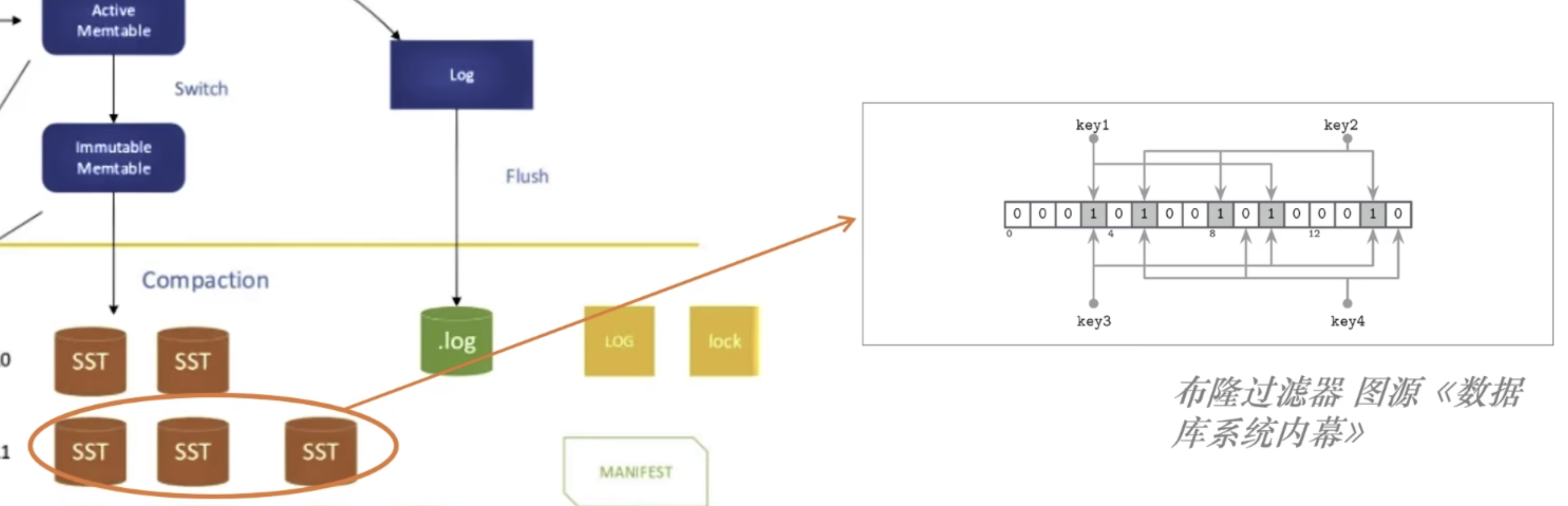
Bloom Filter 用来筛选一层中是否包含我们要查找的数据;
注意到,它可能会返回假阳性的结果,也就是返回一个 key 在这一层,但是实际查找下来是不存在的!但是一定不会返回假阴性的结果!
即:如果 Bloom Filter 返回一个 key 不在这一层,那么这个 key 一定是不存在的!
Bloom Filter的原理实际上也很简单:
就是对每个 key 做 hash 操作,做成一个 bytes 映射数组;
然后对要查找的 key 也进行同样的 hash 操作,然后和 bytes 映射数组比对即可;
通常,如果只有一个 Hash 函数的话,Hash 值重合的概率比较高,误报率较高;
因此,可以设置多个 Hash 函数,这样进来一个 key 的话,只有所有 bytes 映射都命中,才需要真正查询,可以极大程度上降低误报率!
但是如果 Hash 函数过多,Bloom Filter 的代价就会过大,占用的内存也会增多;
因此需要好好协调,这里是一个重要的调参方向;
合并策略(Merging Policy)
上面讲述的是目前主流的 LSM Tree 的实现,本小节来简单介绍一下另一些 LSM Tree 的实现和探索;
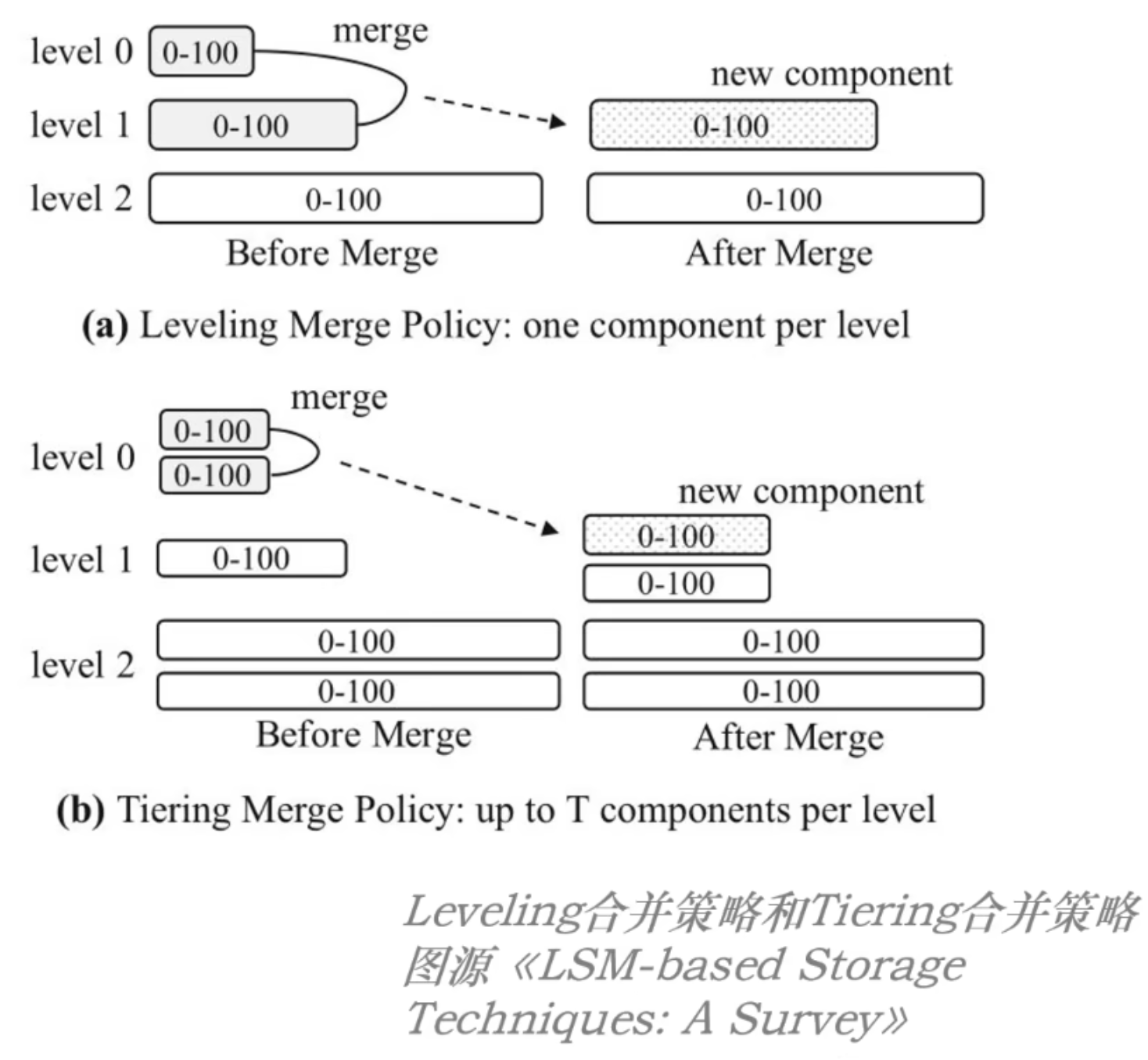
LevelDB 等一系列 LSM Tree 实现采用的方法都是 Leveling Merge Policy 方法;
如上图(a),Leveling 合并策略就是将相连两层的数据做合并,然后一起写入下面一层;
而除此之外,还有另一种合并策略,就是图(b),Tiering Merge Policy;
Tiering 合并策略的每一层都有多个重叠的组件,合并时也并非将相连两层合并,而是将一层中所有组件进行合并,并放入下一层;
相比于 Leveling 合并策略,Tiering 合并策略显而易见的对写入更加友好,但读取的性能会进一步降低:因为每一层也有多个重叠的区域,查找时都是要查找的!
Cassandra 数据库使用的便是 Teiring 合并策略;
LSM-Tree并发控制机制
总体来讲,LSM Tree 因为其天然的 Out-of-place update 特性,在并发控制方面的问题比 BTree 少很多!
对于 LSM Tree 而言,关注的重点主要在于会引起结构变更的操作:
- Memtable 落盘;
- Compaction 过程;
在早期只有一个 Memtable 的情况下,Memtable 的落盘会造成一段时间的不可写!
目前,区分 active memtable 和 immutable memtable 的设计就能在很大程度上避免 memtable 落盘造成的问题;
一些Compaction优化方案
Compaction 一种都是 LSM Tree 的瓶颈所在:
Compaction 过程中占用大量资源,并调整数据位置,同时会引发缓冲池中数据的大量丢失,影响 LSM Tree 结构的读取性能,严重情况下,还可能会造成写停顿(Write Stall)!
因此,关于 Compaction 的优化一直也是 LSM 领域的关注重点!
使用 Tiering 合并策略是提升综合写性能、减少写放大的一个重要手段;
还有另外一些手段来优化 Compaction:
- 采用流水线技术:将读取、合并、写入三个操作以流水线的形式执行,以增强合并操作的资源利用率,减少耗时;
- 复用组件:在合并的过程中识别出不变的部分并保留;
- 主动更新Cache:在 Compaction 结束后主动更新 Cache,或采用机器学习的方式预测回填;
- 单独硬件执行Compaction:把 Compaction 操作 Offload 到例如 FPGA 等额外的硬件上执行;
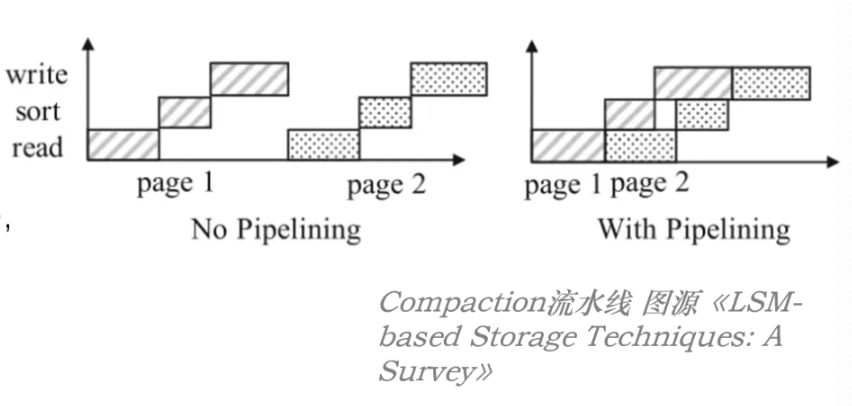
附录
视频地址: