Golang给了我们更加方便和简洁的语法实现并发操作,但是使用并发操作是需要考虑应用场景的,不考虑背景而滥用并发反而可能造成性能危机:有时并发操作并不一定比单线程的效率高;
本文首先通过素数筛方法并发计算质数,展现了golang以CSP为并发模型的并发编程特色;之后与单线程实现做对比,引出并发编程需要考虑背景的结论;
源代码:https://github.com/JasonkayZK/Go_Learn/tree/prime
golang并发素数筛-并发真的会快吗?
前言
最近在看《Go语言高级编程》其中在讲述并发模型时给出了一个Go语言通过并发实现的素数筛计算质数的例子,基本上体现了Golang以CSP为并发模型的并发编程特色;
什么是素数筛
埃拉托斯特尼筛法,简称埃氏筛,也称素数筛,是一种简单且历史悠久的筛法,用来找出一定范围内所有的素数
所使用的原理是从2开始,将每个素数的各个倍数,标记成合数。一个素数的各个倍数,是一个差为此素数本身的等差数列。此为这个筛法和试除法不同的关键之处,后者是以素数来测试每个待测数能否被整除;
简单来说就是:后一个素数在计算时只需根据能否整除前面的素数(过滤)来判断是否是质数即可!
例如:
已经计算了质数序列:2,3,5,7,11,13;
则在计算下一个质数时,只需判断该数可否被2,3,5,7,11,13整除即可,如果都不能被整除,则该数就是下一个质数,如17;
然后将17加入质数堆,继续判断……;
了解了什么是素数筛,下面我们来看看如何使用goroutine配合channel实现一个并发的素数筛;
并发的素数筛
下面是《Go语言高级编程》中提供的一个并发的素数筛;
func GenerateNaturalSeq() chan int {
ch := make(chan int)
go func() {
for i := 2; ; i++ {
ch <- i
}
}()
return ch
}
func AddPrimeFilterChan(in <-chan int, prime int) chan int {
out := make(chan int)
go func() {
for {
if i := <-in; i%prime != 0 {
out <- i
}
}
}()
return out
}
func PrintPrimeN(n int) {
ch := GenerateNaturalSeq()
for i := 0; i < n; i++ {
prime := <-ch
fmt.Printf("%d: %d\n", i, prime)
ch = AddPrimeFilterChan(ch, prime)
}
}其中:
由 GenerateNaturalSeq() 函数不断产生自然数序列,从2开始;
也可以将GenerateNaturalSeq()函数看作是一个没有任何过滤条件的FilterChan
将生成的自然数序列通过 AddPrimeFilterChan() 对(上一个channel产生的)自然数进行过滤;
AddPrimeFilterChan()每次启动会初始化并添加一个新的channel,作为下一个筛子的输入管道:当有新的自然数过来的时候,由最开始生成的筛子过滤,如果不能被该筛子整除,则通过该筛子初始化的时候的管道将自然数传递到下一级筛子,知道最大筛子也无法整除,则判定为素数,输出!
过滤过程如下图:
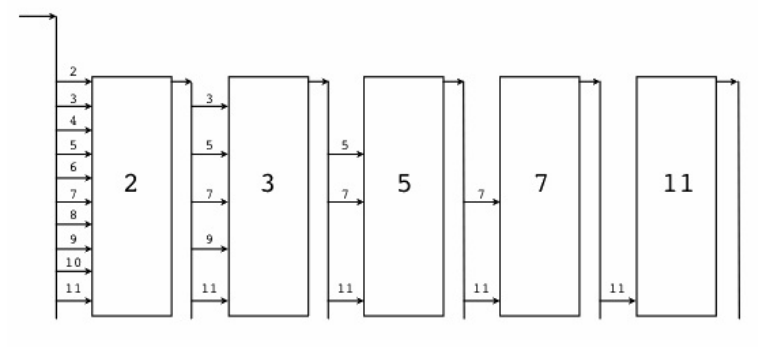
其中:图中大方块代表一个filter,对应于代码中的一个Channel;
注意:
AddPrimeFilterChan() 函数的goruntine内是一个死循环,意思就是会一直运行,直到程序退出
最终调用 PrintPrimeN(n int) 函数计算第n个质数是多少(2是第0个质数);例如调用PrintPrimeN(50)输出如下:
0: 2
1: 3
2: 5
3: 7
4: 11
...并发素数筛的优化
上述并发代码是否有可以优化的空间?
答案是肯定的!
可以从一下几个地方入手:
1.素数肯定不是偶数:所以前面生成的自然数序列可以每次加2;
2.判断整除时只需判断到sqrt(n):假设存在素数n,如果 aa > n,如果 n 能被正整数 x 整除,结果为y,则 x < a 或y < a;所以在过滤正整数 n 时候判断当前素数的平方大于 n,且无法被整除的时候,则可以结束判定;*(此时我们可以直接将n跳过中间的过滤器,直接到达最后一个过滤器)**
实现的代码如下:
// The max value of the prime filter
// Update only when new prime filter added
var MaxFilter chan int
func NewGenerateNaturalSeq() chan int {
ch := make(chan int)
go func() {
for i := 3; ; i += 2 {
ch <- i
}
}()
return ch
}
func NewAddPrimeFilterChan(in <-chan int, prime int) chan int {
out := make(chan int)
MaxFilter = out
go func() {
for {
if i := <-in; i%prime != 0 {
// Boundary condition:
// Pass the i to the last filter
if i < prime*prime {
MaxFilter <- i
} else {
out <- i
}
}
}
}()
return out
}
func NewPrintPrimeN(n int) {
ch := NewGenerateNaturalSeq()
fmt.Println("0: 2")
for i := 1; i < n; i++ {
prime := <-ch
fmt.Printf("%d: %d\n", i, prime)
ch = NewAddPrimeFilterChan(ch, prime)
}
}调用NewPrintPrimeN(50)输出如下:
0: 2
1: 3
2: 5
3: 7
4: 11
...单线程素数筛
上面展示了并发实现素数筛的方法,下面提供一个简单的单线程实现的素数筛,同样使用了上述说的优化,代码如下:
var filter []int
func SerialPrintPrimeN(n int) {
filter = make([]int, 0, n+1)
fmt.Println("0: 2")
for prime, i := 3, 1; i < n; prime += 2 {
if FilterPrime(prime) {
filter = append(filter, prime)
fmt.Printf("%d: %d\n", i, prime)
i++
}
}
}
func FilterPrime(x int) bool {
for _, f := range filter {
if x < f * f {
return true
}
if x % f == 0 {
return false
}
}
return true
}代码通过filter切片记录了需要过滤的质数(已经检测的质数),每次通过filter切片对下一个数进行过滤,并且在成功判断一个质数之后,将该质数也加入到filter切片中作为过滤条件;
有点类似于DP的思想
最终,执行FilterPrime(50),也可以正确输出质数:
0: 2
1: 3
2: 5
3: 7
4: 11
...性能比较
上面的三种方法都可以计算第n个质数,那么究竟各个方法的性能如何呢?
下面的方法通过计算第50000个质数比较了三个方法的性能:
func main() {
t1 := time.Now().UnixNano()
prime.SerialPrintPrimeN(50000)
t2 := time.Now().UnixNano()
fmt.Printf("serial time: %d ms\n", t2 - t1)
prime.PrintPrimeN(50000)
t3 := time.Now().UnixNano()
fmt.Printf("parallel time: %d ms\n", t3 - t2)
prime.NewPrintPrimeN(50000)
fmt.Printf("new parallel time: %d ms\n", time.Now().UnixNano() - t3)
}最终的输出为:
serial time: 56817800 ns
parallel time: 118040981000 ns
new parallel time: 2170814700 ns优化后的并发素数筛比优化前快了118040981000/2170814700 = 54倍;
而单线程比多线程快了2170814700/56817800 = 38倍!
结论
为什么单线程要比多线程的版本快呢?
答案是显而易见的:
单线程避免了多线程上下文切换的时间;而在高并发下,每一个协程还是需要等待由其他协程通过channel传递而来的值
原因是:在判断素数序列时,必须等待序列中的前一个数完成是否为素数的判断后才可以判断序列中的下一个数,即:这个解决方案本身就是序列化的(后一个问题的结果建立在前一个问题的结果之上);所以此解决方案并不适合使用并发来实现!
通常高度并行化的问题更适合使用并发来解决(类似于分治或者MapReduce思想),例如:
- 区间求和可以将区间划分为子区间分别求和;
- 数组求取最大值等;
相信通过上面的例子,你一定对Go中的并发模型特色有了一个深刻的认识!
但是即便Go给我们提供了如此便捷的并发编程体验,我们也应当对应实际的场景来谨慎使用并发;(《Go语言高级编程》所提供的例子也只是为了体现在Go中并发编程的特点)
附录
源代码:https://github.com/JasonkayZK/Go_Learn/tree/prime
如果觉得文章写的不错, 可以关注微信公众号: Coder张小凯
内容和博客同步更新~
